Bâtir et analyser un plan d’expériences de Surface de Réponse avec CORICO
Le logiciel CORICO n’est pas seulement un générateur de plan d’expériences, c'est aussi un outil d’analyse convivial et rapide, applicable aussi bien à un plan généré par lui-même que par un autre logiciel.
la méthode des surfaces de réponses vise à trouver les relations entre les variables dépendantes et indépendantes impliquées dans une expérience. Le plus souvent on utilise un modèle à polynôme de second degré. La méthode CORICO permet d’aller plus loin , en intégrant aux modèles des « interactions logiques », pour une prédiction plus robuste et proche de la réalité.
L'objectif est de déterminer plus vite l'optimum de la réponse (la ou les variables dépendantes).
L'exemple d'un plan industriel
Un industriel cherche, en fonction de 5 facteurs A, B, C, D, E, à maximiser une réponse « yy » qui joue un rôle crucial en termes de qualité et, donc, de coût de fabrication, à cause des rebuts et des réclamations clients.
Bâtir le plan d’expériences
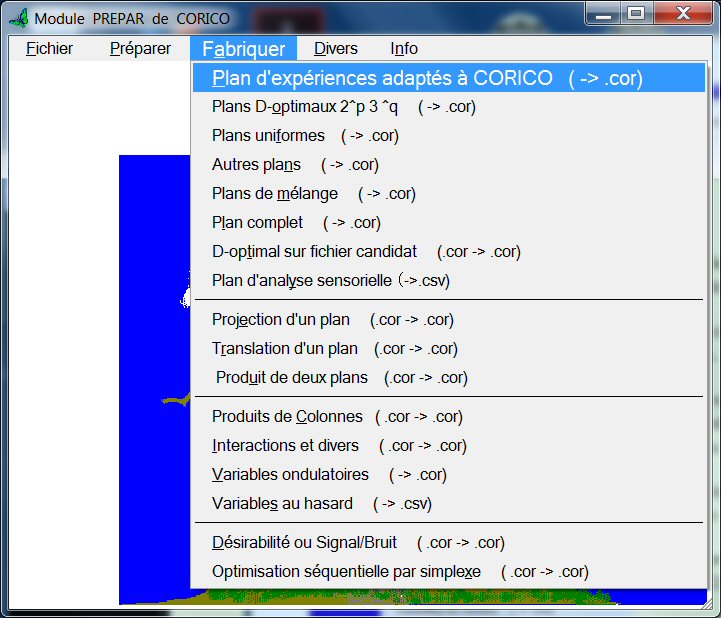
Dans le module « PREPAR » de CORICO, sélectionnez le menu Fabriquer :
Beaucoup de plans sont disponibles dans ce menu (composite centré, Box Behnken, Doehlert, etc.
Nous sommes novices en la matière et nous ne postulons pas de modèle a priori (ce n’est jamais nécessaire avec CORICO).
Choisissons donc un plan à tout faire et sans risque :
cliquons sur « Plan d’expériences adaptés à CORICO ».
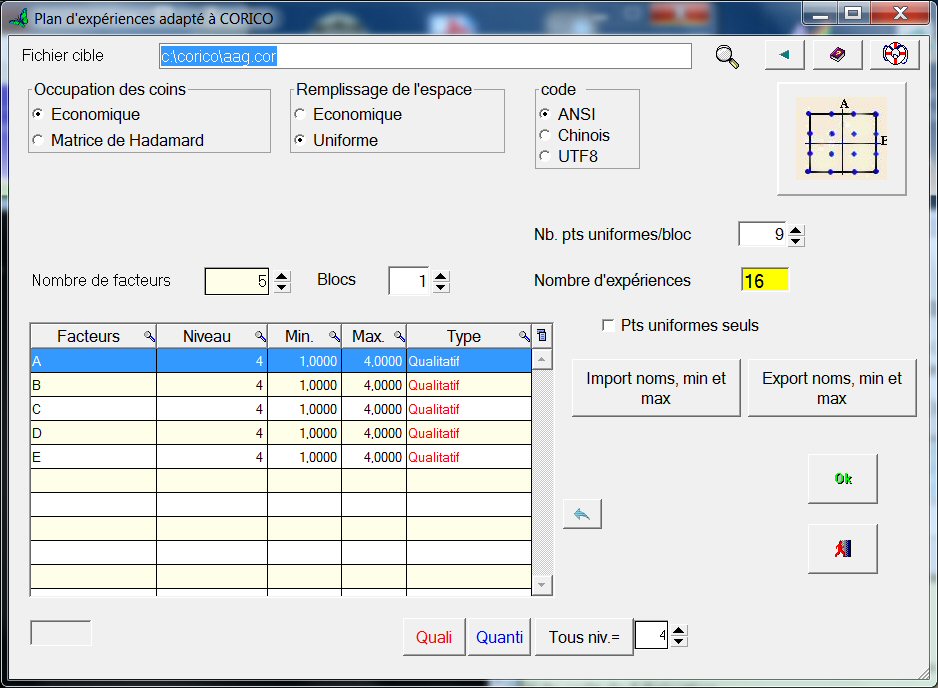
Pour étudier précisément l’intérieur du domaine expérimental, choisissons 4 niveaux par facteur.
Nos facteurs sont quantitatifs (continus) ; en principe il suffit d’inscrire « Quantitatif » dans la colonne « Type ». On obtient des points équidistants dans l’espace à 5 dimensions (5 facteurs). Par suite, les niveaux de chaque facteur ne sont pas équidistants en projection sur le plan de deux facteurs. Un tel plan d'expériences est tout à fait correct.
Choisissons cependant ici le type « qualitatif », afin d’avoir des niveaux équidistants pour chaque facteur séparément (le type « qualitatif » peut servir aussi bien pour les facteurs quantitatifs que pour les facteurs qualitatifs).
Donnons un nom au fichier (ici aag.cor), puis cliquons OK. Le plan est créé.

Ce plan n’a que 16 essais, ce qui est très économique pour 5 facteurs à 4 niveaux. Il est dit « plan de surface de réponse », car les facteurs ont plus de deux niveaux, afin d'appréhender les effets non linéaires.
La figure ci-contre montre la répartition des points dans le domaine expérimental, quel que soit le couple de 2 facteurs.
On réalise les 16 expériences, puis l'on reporte les mesures de la réponse yy dans le fichier aag.cor :
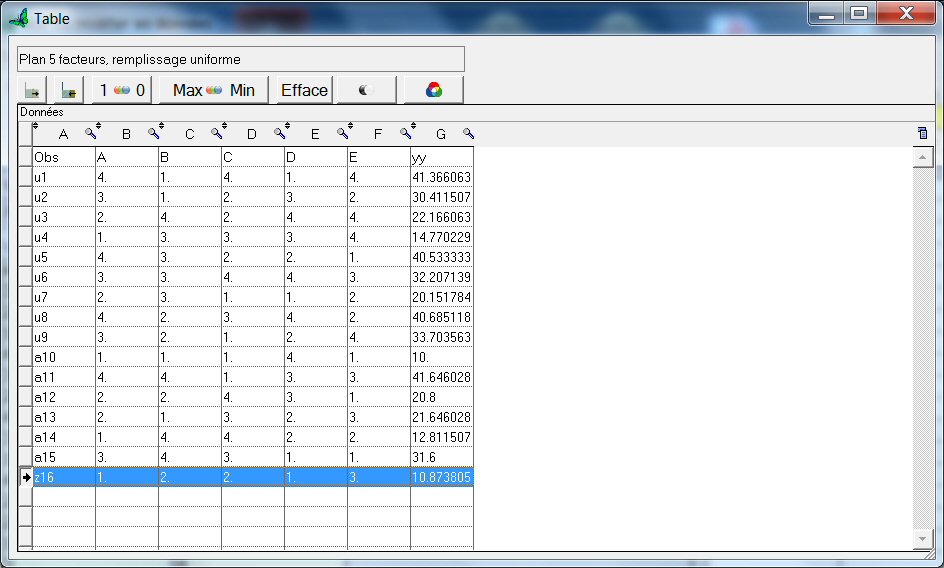
Analyse des résultats des expériences
Dans le menu Outils de CORICO, sélectionnons « MODELE régression multiple, série chronologique » :
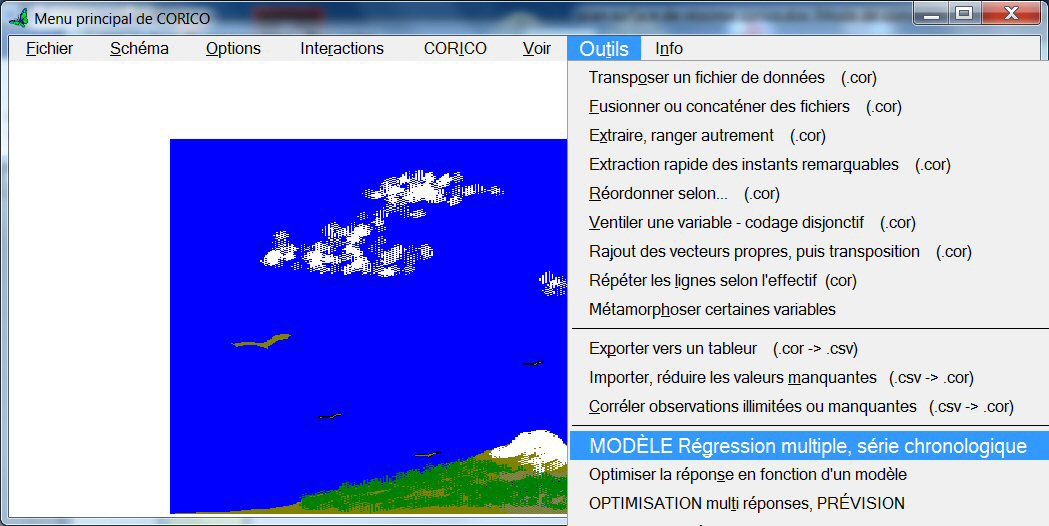
Sélectionnons le fichier aag.cor qui contient notre plan :
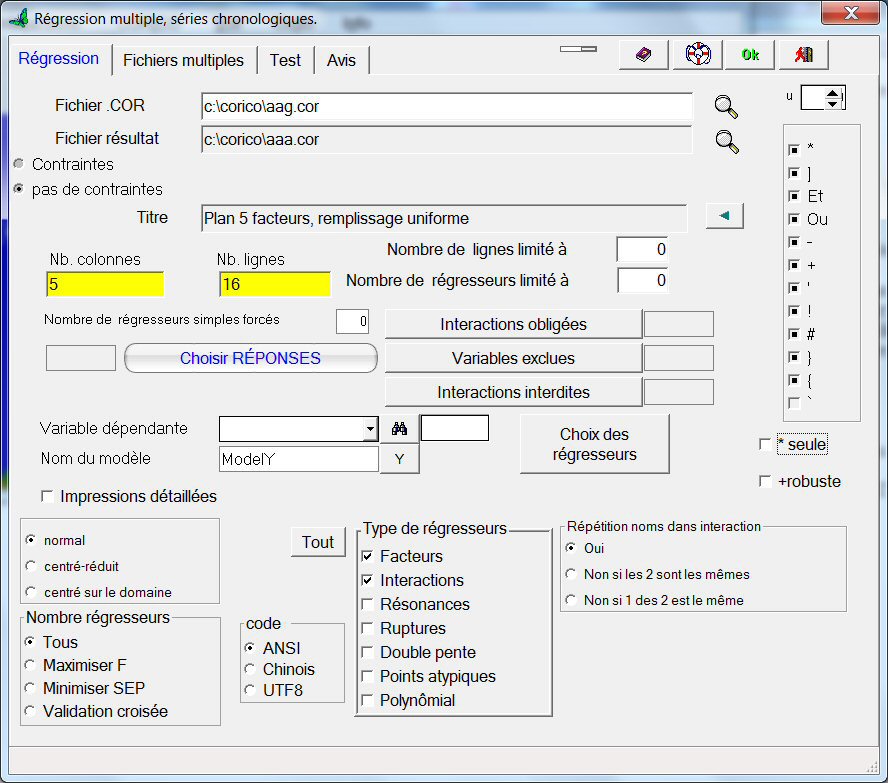
Cliquons sur le bouton « Choisir REPONSE », et sélectionnons yy :
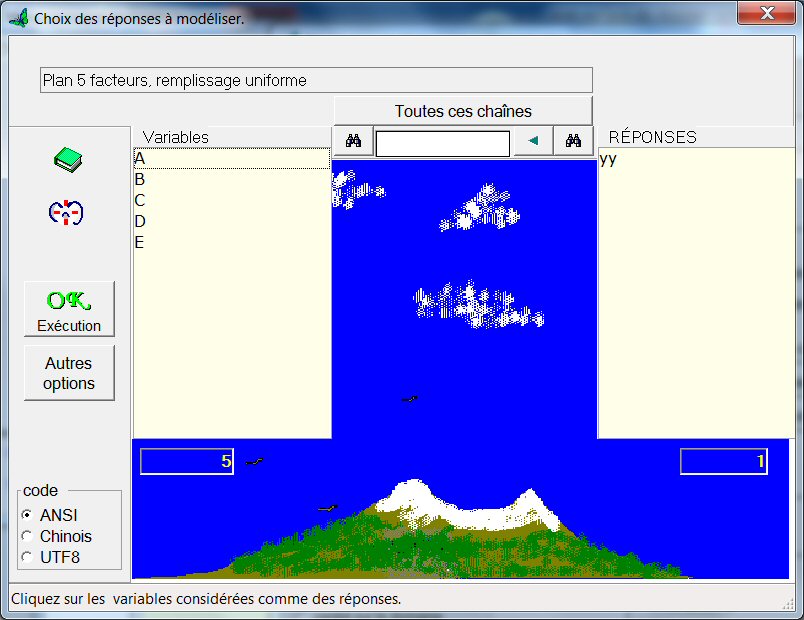
Puis cliquons OK. Le modèle de yy avec « interactions logiques » est créé (modèle 1) :

Le modèle 1 n’est pas postulé à priori : c'est l'algorithme de CORICO qui détermine les termes du modèle par ordre décroissant d’importance, chacun expliquant le résidu non expliqué par les précédents.
Les coefficients R2 ajustés, Q2 et F sont excellents. SEP est l’erreur standard de prédiction.
Les modèles de type CORICO avec « interactions logiques » sont souvent plus parcimonieux que les modèles polynomiaux classiques, c’est-à-dire que les termes du modèle (régresseurs) sont moins nombreux (il n’y a ici que 6 coefficients, y compris la constante).
En outre, les modèles avec « interactions logiques » peuvent s'ajuster à des surfaces de réponses beaucoup plus variées et "tourmentées".
Optimisation de la réponse
A partir du modèle précédent, on cherche à maximiser yy.
Cliquons au menu Outil…OPTIMISATION multiréponse, PREVISION :
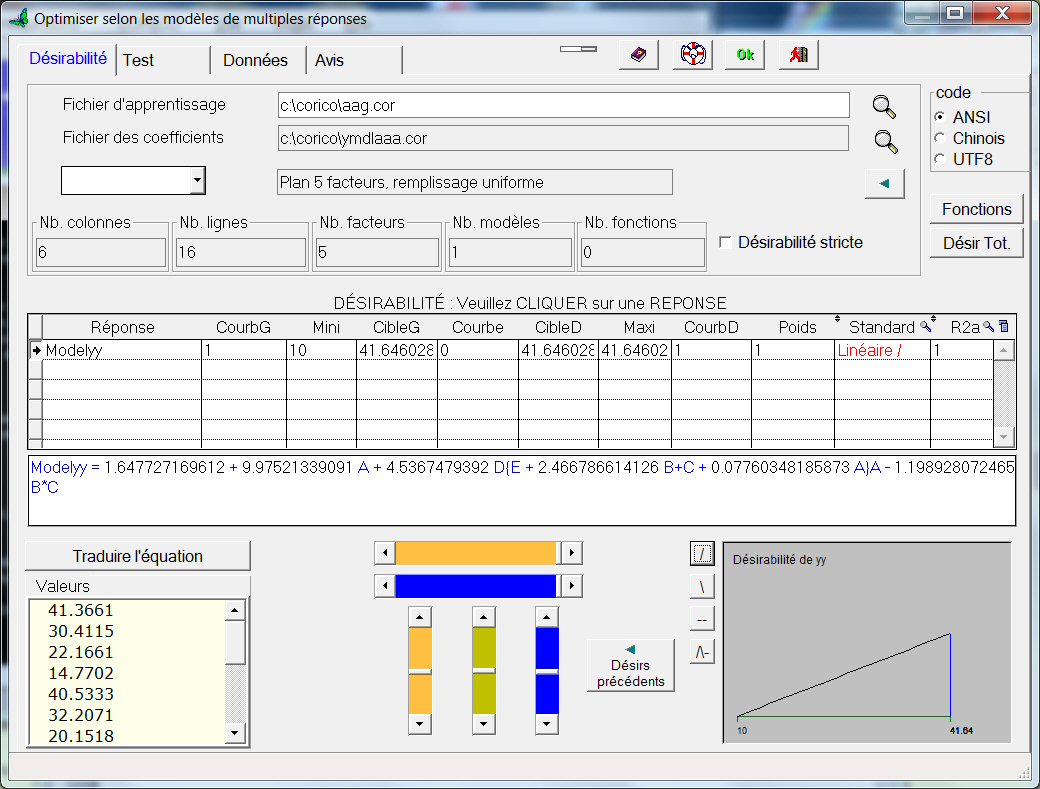
On a choisi un graphe de désirabilité qui maximise yy.
Cliquons sur l’onglet « Test » puis sur le bouton « Optimisation » :
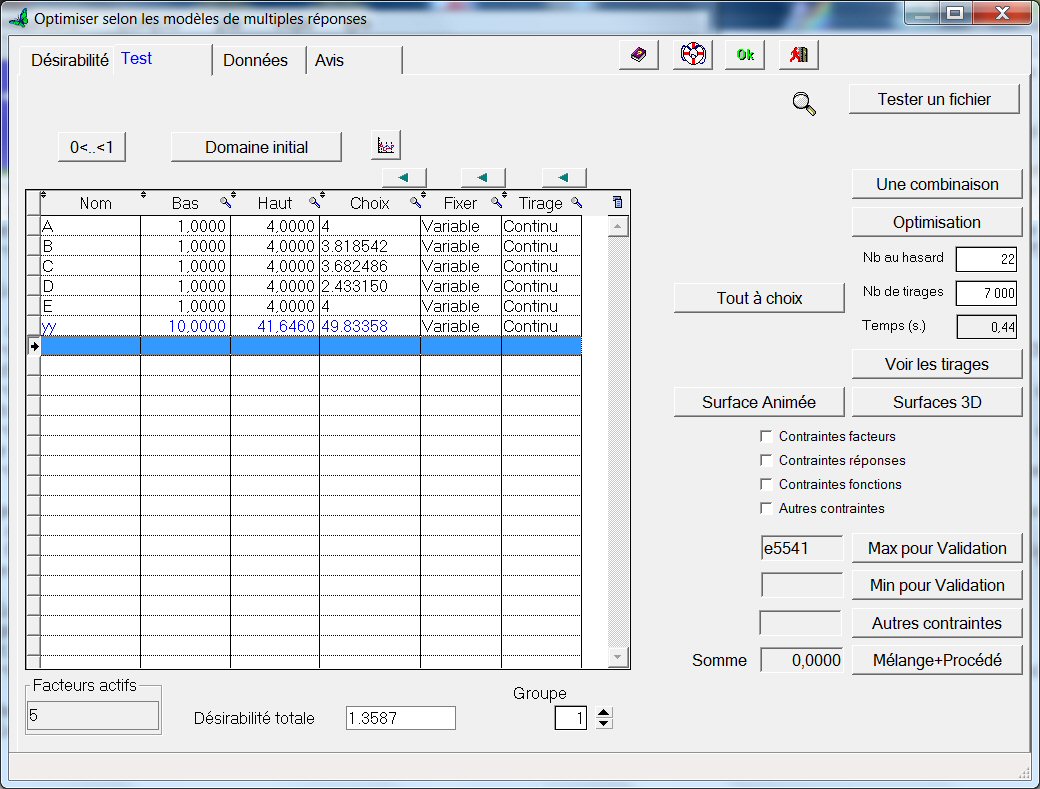
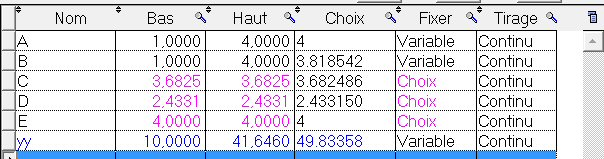
Après un tirage de Montecarlo, la colonne « Choix » contient les valeurs des facteurs qui maximisent la réponse. Ces valeurs pourront faire l’objet d’un essai de validation.
Comme il y a 5 facteurs, il est difficile de tracer une surface de réponse. Nous ne ferons donc varier que les deux premiers facteurs A et B, en fixant les autres à leurs valeurs de la colonne choix :
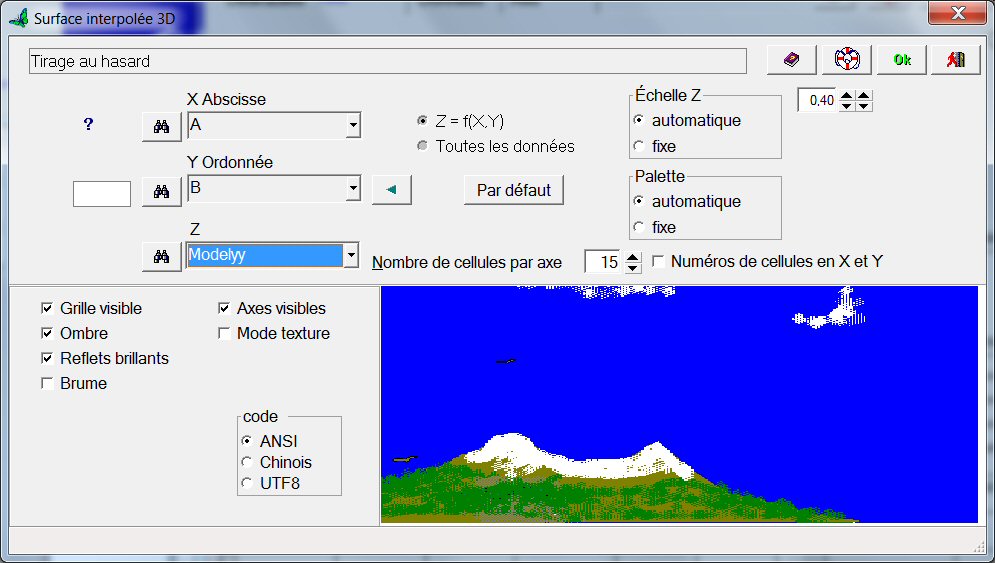
Appuyons à nouveau sur le bouton « Optimisation », puis cliquons sur le bouton « Surface 3D ». Choisissons A et B respectivement en X et Y, et le modèle de yy en Z :
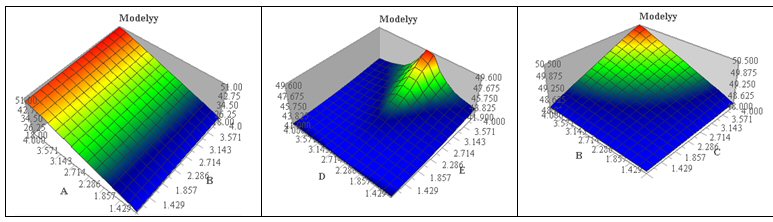
Cliquons OK : nous obtenons la surface de réponse de yy quand A et B varient seuls.
Procédons de même pour la surface de réponse de yy quand D et E varient seuls, et pour la surface de réponse de yy quand B et C varient seuls :
Comparaison avec un modèle polynomial classique
Si nous excluons la recherche d'interactions logiques, nous obtenons un modèle polynomial classique (modèle 2) :

Le modèle semble, au vu des coefficients R2a et Q2 presque aussi bon que le précédent. Cependant l’erreur standard de prédiction SEP est presque multipliée par 18 !
D’autre part le tableau d’optimisation est maintenant :
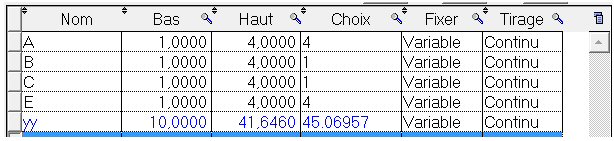
La variable D n’apparaît pas, puisqu’elle ne fait pas partie du modèle. Or elle jouait un rôle crucial dans le modèle 1 (interaction D{E deuxième par ordre d’importance}.
Le maximum trouvé pour yy est maintenant 45,06 au lieu de 49,83. D’autre part, les valeurs trouvées pour A, B, C et E, dans la colonne choix, diffèrent de celles trouvées avec le 1er modèle.
Un essai de validation sera donc nécessaire pour départager les deux modèles.
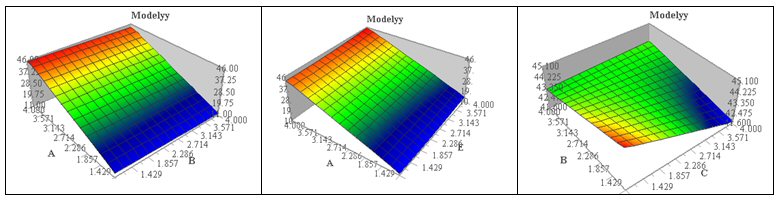
En attendant, traçons comme précédemment les surfaces de réponses. (On n’a pas pu tracer yy en fonction de D et E puisque D est absent du modèle 2. La surface de réponse de yy en fonction de B et C est très différente de celle que donne le modèle 1.
Conclusion de l'analyse
Il y a tout lieu de penser que le modèle 1 colle mieux avec la réalité, car les interactions logiques ont un sens physique très fort. De plus le modèle 2 néglige l’influence de D, et l'erreur standard de prédiction est presque 18 fois plus forte.
Une fois les modèles départagés, au vu des essais de validation, le réglage optimum des paramètres A, B, C, D et E, en fabrication, devrait dégager un profit important pour l’usine.
Mais comment les autres ingénieurs de l’usine vont-ils pouvoir utiliser le modèle retenu s’ils ne possèdent pas eux aussi le logiciel CORICO ? Pas de problème : le logiciel est accompagné d’un utilitaire gratuit qui permet à chacun d’utiliser le modèle, y compris s’il contient des interactions logiques.
Voir aussi : Questions fréquentes.
D'autres exemples d'analyse de données avec CORICO :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.
Economisez des années en Recherche et Développement :
INDUSTRIE - RECHERCHE - QUALITÉ - ÉPIDÉMIOLOGIE - ENQUÊTES - ECONOMETRIE ...
FORMATION
- Découvrir et maîtriser
- l'Analyse de Donnéees
- le Plan d'expériences
- les Séries Temporelles
- Voir les formations