Analyse des Iris de Fisher
"Les iris de Fisher" sont des données fameuses collectées par Edgar Enderson, et proposées en 1933 par le statisticien Ronald Aylmer Fisher comme données de référence pour l'analyse discriminante et la classification. Le fichier est accessible sur de nombreux sites Internet.(Par exemple).
Il s’agit de reconnaître le type d’iris (setosa, virginica, et versicolor) à partir seulement de la longueur et de la largeur de ses pétales et sépales. Le fichier contient 50 fleurs de chaque type.
L'iconographie des corrélations permet une analyse rapide et simple de ce fichier.
C'est une alternative à l'Analyse en Composantes Principales (ACP) ou à l’analyse factorielle discriminante (AFD). Dans l’AFD, il y a une variable qualitative à expliquer (ici le type d’iris) et p variables quantitatives explicatives (ici longueurs et largeurs des pétales et des sépales).
A noter que l’iconographie des corrélations est plus générale en ce que vous pouvez avoir plusieurs variables à expliquer (qualitatives ou quantitatives), et des variables explicatives qualitatives et/ou quantitatives.
Iconographie des corrélations
Voici la figure obtenue par le logiciel CORICO. Les variables indicatrices des trois espèces d’Iris sont en rouge :
Elle donne le résultat suivant, où un trait plein représente une corrélations remarquables positive, et un trait pointillé indique une corrélation remarquables négative. Les espèces d'Iris sont en rouge :
La figure synthétise graphiquement de façon immédiate et claire l’ensemble des informations suivantes :
Iris-Setosa se caractérise par
Iris-Virginica se caractérise par
Iris-Versicolor s’oppose aux deux précédentes espèces et se caractérise par
La même figure montre aussi que, dans ce corpus de données, les longs pétales sont en général associés à des larges pétales et à de longs sépales (donc ces grandeurs varient plutôt proportionnellement).
D’autres représentations graphiques des iris de Fisher telles que nuage de points, diagrammes en bâton, etc. sont possibles, mais elles ne nous apprendraient guère plus, et alourdiraient la lecture des résultats. Ces représentations sont moins commodes encore si le nombre de variables augmente. Avec l’iconographie des corrélations, au contraire, il est toujours possible d’obtenir une figure claire, car l'interprétation repose sur les liens. Par exemple, en présence de milliers de variables quantitatives ou qualitatives (catégorielles), il suffit de ne dessiner que les liens à la variable d’intérêt.
Iconographie des corrélations du tableau transposé
Retirons du tableau de données les 3 variables indicatrices des espèces, afin de travailler en aveugle, puis transposons le tableau de données (les lignes deviennent les colonnes et réciproquement) :
L’iconographie des corrélations donne ici, schématiquement, sur la sphère de CORICO, les relations entre les fleurs particulières. Le logiciel a bien décelé trois groupes.
Il y a cependant des passerelles entre les groupes : si l’on colore en rouge les Sétosa, en vert les Versicolor, et en bleu les Virginica, il apparaît que quelques-unes de ces dernières se sont placées avec le groupe des Sétosa et quelques autres avec les versicolores. En revanche aucune des Setosa ne va se placer dans les autres groupes. Ce sont donc les fleurs les plus facilement reconnaissables au vu des seuls pétales et sépales.
Analyse en composantes principales (ACP)
Le logiciel CORICO donne aussi l’analyse en composantes principales :
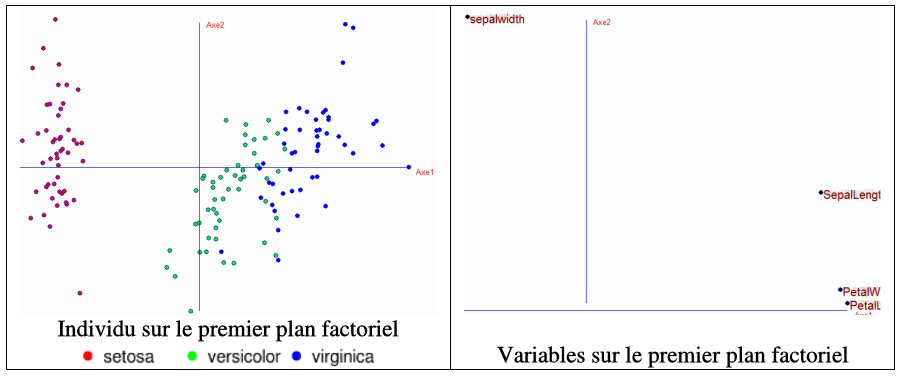
On retrouve les mêmes résultats : L’axe 1 oppose PetalWidth, PetalLength et SepalLength (à droite) à SepalWidth (à gauche). les Setosa sont bien séparées à gauche.
Intérêts de l’iconographie des corrélations par rapport à l’ACP :
Classification croisée
Le logiciel CORICO fournit aussi la classification croisée du tableau des Irish de Fisher, c’est-à-dire le rangement des lignes et des colonnes.
Le tableau d’origine contient 4 colonnes (SepalLength, SepalWidth, PetalLength et PetalWidh) et 149 lignes. Les colonnes ont été ramenées à une unité commune d’évaluation (par exemple centrée réduites).
Colorons les cellules du tableau en fonction des valeurs (rouge pour les plus fortes valeurs, bleu pour les plus faibles, et couleurs intermédiaires). La figure suivante montre le tableau avant rangement et après rangement :

Après classification croisée, la colonne de gauche est SepalWidth, très différente des trois colonnes suivantes SepalLength, PetalLength et PetalWidth.
Les premières lignes regroupent tous les Setosa.
Les lignes suivantes regroupent les Versicolor et les VIrginica qui ne sont pas aussi bien séparées que dans les méthodes précédentes. La classification croisée est moins précise et moins générale.
Modèles de régression multiple de type « CORICO »
Si maintenant l’on souhaite, non seulement décrire, mais aussi prédire le type d’Iris de FIsher d’après les dimensions de ses pétales et sépales, le logiciel CORICO propose les modèles suivants :
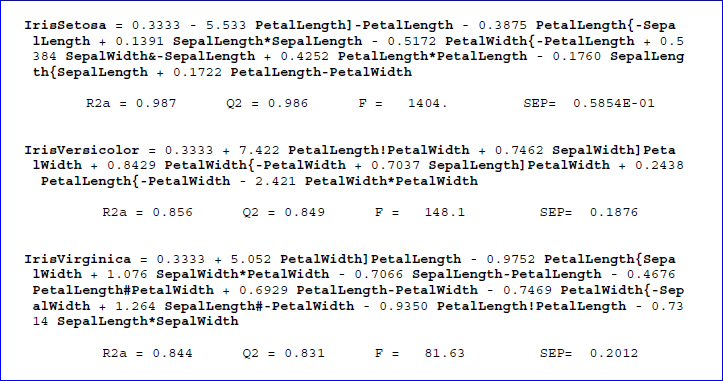
Un modèle de type CORICO peut faire fait intervenir, outre des termes polynomiaux, des « interactions logiques » qui ont un « sens physique » très fort ; d’où des modèles qui collent généralement mieux avec la réalité. De plus les termes sont rangés par importance décroissante.
La qualité de l’ajustement du modèle aux données réelles est évaluée au moyen du « R2 ajusté » (R2a), et du « R2 prédictif » (Q2), lesquels doivent être le plus proches de 1 possible, une erreur standard de prédiction (SEP) est calculée dans l’unité de la variable modélisée. Le coefficient F est le rapport de la fraction expliquée par le modèle sur la fraction résiduelle. Il doit être le plus grand possible.
Ici, ces coefficients sont relativement bons, surtout pour Iris-setosa.
Règles de segmentation pour l’espèce Iris-Setosa
A titre indicatif, CORICO propose aussi les règles suivantes (pas forcément utiles pour l'interprétation) :
REGLE LOCALE n°1
Si PetalLength entre 3.0000 et 6.9000
et PetalWidth entre 1.0000 et 2.5000
alors IrisSetosa entre 0.0000 et 0.0000
0 contre-exemple(s) 100 observations 0 confirmations
Pureté pratique 100.00%, généralité 100.00 %, largeur= 0.64, robustesse=100.00
Groupe +1= +(PetalLength]-PetalLength)
REGLE LOCALE n°2
Si PetalLength entre 1.0000 et 1.9000
et PetalWidth entre 0.10000 et 0.60000
alors IrisSetosa entre 1.0000 et 1.0000
0 contre-exemple(s) 50 observations 0 confirmations
Pureté pratique 100.00%, généralité 100.00 %, largeur= 0.18, robustesse=100.00
Groupe -1= -(PetalLength]-PetalLength)
L’espèce Iris-Setosa est la plus aisée à reconnaître parmi les iris de Fisher, car il n’y a que deux règles : 1. Celle qui conclut que la fleur n’est pas Iris-Setosa, et 2. celle qui conclut que la fleur est Iris-Setosa.
Règles de segmentation pour l’espèce Iris-Versicolor
Pour l’espèce Iris-Versicolor, il y a plus de cas particuliers, donc plus de règles, certaines sont plus robustes ou générales que d’autres :
REGLE LOCALE n°1
Si PetalLength entre 3.0000 et 4.9000
et PetalWidth entre 1.0000 et 1.6000
alors IrisVersicolor entre 1.0000 et 1.0000
0 contre-exemple(s) 47 observations 0 confirmations
Pureté pratique 100.00%, généralité 94.00 %, largeur= 0.29, robustesse=100.00
Groupe +1= +PetalLength!PetalWidth
REGLE LOCALE n°2
Si PetalLength entre 5.0000 et 5.1000
et PetalWidth entre 1.6000 et 1.7000
alors IrisVersicolor entre 1.0000 et 1.0000
0 contre-exemple(s) 2 observations 0 confirmations
Pureté pratique 100.00%, généralité 4.00 %, largeur= 0.03, robustesse= 66.89
Groupe -1+1+1= -PetalLength!PetalWidth+PetalLength!PetalWidth+PetalLength!PetalWidth
REGLE LOCALE n°3
Si SepalLength entre 5.9000 et 5.9000
et SepalWidth entre 3.2000 et 3.2000
et PetalLength entre 4.8000 et 4.8000
et PetalWidth entre 1.8000 et 1.8000
alors IrisVersicolor entre 1.0000 et 1.0000
0 contre-exemple(s) 1 observations 0 confirmations
Pureté pratique 100.00%, généralité 2.00 %, largeur= 0.00, robustesse= 42.26
Groupe -1+1-1+2 -PetalLength!PetalWidth+PetalLength!PetalWidth-PetalLength!PetalWidth+SepalLength{SepalWidth
REGLE LOCALE n°4
Si SepalLength entre 4.9000 et 6.3000
et SepalWidth entre 2.2000 et 3.0000
et PetalLength entre 4.5000 et 5.1000
et PetalWidth entre 1.5000 et 1.8000
alors IrisVersicolor entre 0.0000 et 0.0000
0 contre-exemple(s) 5 observations 3 confirmations
Pureté pratique 100.00%, généralité 5.00 %, largeur= 0.24, robustesse= 64.33
Groupe -1+1-1-2 -PetalLength!PetalWidth+PetalLength!PetalWidth-PetalLength!PetalWidth-SepalLength{SepalWidth
REGLE LOCALE n°5
Si PetalLength entre 1.0000 et 6.9000
et PetalWidth entre 0.10000 et 2.5000
alors IrisVersicolor entre 0.0000 et 0.0000
47 contre-exemple(s) 95 observations 4 confirmations
Pureté pratique 66.90%, généralité 95.00 %, largeur= 1.00, robustesse= 47.02
Groupe -1-1= -PetalLength!PetalWidth-PetalLength!PetalWidth
Règles de segmentation pour l’espèce Iris-Virginica
Cette fois, 8 règles ont été nécessaires.
REGLE LOCALE n°1
Si SepalLength entre 6.5000 et 6.7000
et SepalWidth entre 2.5000 et 3.0000
et PetalLength entre 5.5000 et 5.8000
et PetalWidth entre 1.8000 et 1.8000
alors IrisVirginica entre 1.0000 et 1.0000
0 contre-exemple(s) 2 observations 0 confirmations
Pureté pratique 100.00%, généralité 4.00 %, largeur= 0.08, robustesse= 66.89
Groupe +1+3+5= +PetalWidth]PetalLength+(SepalLength{-PetalWidth)+PetalWidth
REGLE LOCALE n°2
Si SepalLength entre 6.7000 et 6.7000
et SepalWidth entre 3.0000 et 3.0000
et PetalLength entre 5.0000 et 5.0000
et PetalWidth entre 1.7000 et 1.7000
alors IrisVirginica entre 0.0000 et 0.0000
0 contre-exemple(s) 1 observations 0 confirmations
Pureté pratique 100.00%, généralité 1.00 %, largeur= 0.00, robustesse= 18.35
Groupe +1+3-5= +PetalWidth]PetalLength+(SepalLength{-PetalWidth)-PetalWidth
REGLE LOCALE n°3
Si SepalLength entre 5.9000 et 5.9000
et SepalWidth entre 3.2000 et 3.2000
et PetalLength entre 4.8000 et 4.8000
et PetalWidth entre 1.8000 et 1.8000
alors IrisVirginica entre 0.0000 et 0.0000
0 contre-exemple(s) 1 observations 0 confirmations Pureté pratique 100.00%, généralité 1.00 %, largeur= 0.00, robustesse= 18.35 Groupe +1-3+4+7 +PetalWidth]PetalLength-(SepalLength{-PetalWidth)+(SepalWidth&-PetalLength)+(SepalWidth{-SepalLength)
REGLE LOCALE n°4
Si SepalLength entre 5.9000 et 7.2000
et SepalWidth entre 3.0000 et 3.6000
et PetalLength entre 4.8000 et 6.1000
et PetalWidth entre 1.8000 et 2.5000
alors IrisVirginica entre 1.0000 et 1.0000
0 contre-exemple(s) 17 observations 7 confirmations
Pureté pratique 100.00%, généralité 34.00 %, largeur= 0.28, robustesse=100.00
Groupe +1-3+4-7 +PetalWidth]PetalLength-(SepalLength{-PetalWidth)+(SepalWidth&-PetalLength)-(SepalWidth{-SepalLength)
REGLE LOCALE n°5
Si SepalLength entre 4.9000 et 7.9000
et SepalWidth entre 2.5000 et 3.8000
et PetalLength entre 4.5000 et 6.9000
et PetalWidth entre 1.6000 et 2.5000
alors IrisVirginica entre 1.0000 et 1.0000
0 contre-exemple(s) 28 observations 19 confirmations
Pureté pratique 100.00%, généralité 56.00 %, largeur= 0.54, robustesse=100.00
Groupe +1-3-4= +PetalWidth]PetalLength-(SepalLength{-PetalWidth)-(SepalWidth&-PetalLength)
REGLE LOCALE n°6
Si PetalLength entre 1.0000 et 4.9000
et PetalWidth entre 0.10000 et 1.6000
alors IrisVirginica entre 0.0000 et 0.0000
0 contre-exemple(s) 97 observations 0 confirmations
Pureté pratique 100.00%, généralité 97.00 %, largeur= 0.64, robustesse=100.00
Groupe -1+2= -PetalWidth]PetalLength+PetalLength*PetalLength
REGLE LOCALE n°7
Si SepalLength entre 6.0000 et 6.0000
et SepalWidth entre 2.7000 et 2.7000
et PetalLength entre 5.1000 et 5.1000
et PetalWidth entre 1.6000 et 1.6000
alors IrisVirginica entre 0.0000 et 0.0000
0 contre-exemple(s) 1 observations 0 confirmations
Pureté pratique 100.00%, généralité 1.00 %, largeur= 0.00, robustesse= 18.35
Groupe -1-2+6= -PetalWidth]PetalLength-PetalLength*PetalLength+SepalLength*PetalWidth
REGLE LOCALE n°8
Si SepalLength entre 6.0000 et 6.3000
et SepalWidth entre 2.2000 et 2.8000
et PetalLength entre 5.0000 et 5.6000
et PetalWidth entre 1.4000 et 1.5000
alors IrisVirginica entre 1.0000 et 1.0000
0 contre-exemple(s) 3 observations 0 confirmations
Pureté pratique 100.00%, généralité 6.00 %, largeur= 0.12, robustesse= 81.14
Groupe -1-2-6= -PetalWidth]PetalLength-PetalLength*PetalLength-SepalLength*PetalWidth
Conclusion
L’iconographie des corrélations fourni des schémas parlants, accessibles à tous. Les modèles non postulés servent à la prédiction.
Les règles de segmentation, facultatives, sont surtout descriptives des différents cas observés, et sauf pour Iris-Setosa, sont moins commodes que les modèles pour la prédiction, et moins commodes que les schémas pour l'interprétation.
Si l’on prenait en compte d’autres caractéristiques des iris, en plus des dimensions des pétales et des sépales, on obtiendrait certainement des règles plus générales et plus précises.
Voir aussi : Questions fréquentes.
D'autres exemples d'analyse de données avec CORICO :