comment éviter l'erreur induite par la moyenne ?
Lorsqu’on compare plusieurs séries d’observations chiffrées, le calcul de la moyenne peut être un moyen de résumer l’information. Mais il ne faut pas en cacher les dangers lorsque l’on s’intéresse aux relations entre les variables.
Un exemple simple
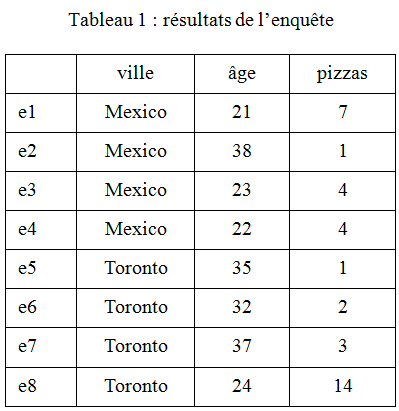
On a interrogé quatre personnes à Mexico, et quatre personnes à Toronto, sur leur âge et le nombre de pizzas achetées dans le mois. Les données brutes de l’enquête sont rassemblées dans le tableau 1.
Le coefficient de corrélation entre l’âge et le nombre de pizzas pour les 8 mesures est négatif (-0.61). Il est également négatif séparément pour Mexico (-0.863) et pour Toronto (-0.905)
Conclusion : les « jeunes » achètent plus de pizza que les « vieux ».
Calculons maintenant les moyennes pour chacune des deux villes (Tableau 2).
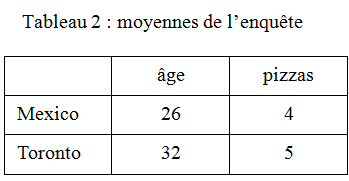
Cette fois, il semble que les « jeunes » achètent moins de pizza : la corrélation entre l’âge et le nombre de pizzas est devenue positive (+1) !
Bien entendu, la corrélation calculée sur les données brutes est la plus sûre, car la moyenne mélange tout. Elle efface beaucoup d’informations. Ici, elle a inversé la relation.
Que se passe-t-il si l'on augmente la taille de l'échantillon de population?
On dira peut-être que l’échantillon est trop faible. Qu’aurait-on obtenu, si l’échantillon avait été un million de personnes dans chaque ville ?
Si l'on admet que :
Alors, nous aurions obtenu le même tableau moyen sur un échantillon d’un million de personnes dans chaque ville, donc une corrélation positive entre l’âge et le nombre de pizzas. C’est-à-dire l’inverse de la réalité.
Conclusion préliminaire
Il est dangereux de calculer des corrélations à partir de moyennes, et c’est d’autant plus inutile ici que nous disposons des données brutes.
La relation est la seule réalité. La mesure est un intermédiaire pour découvrir les relations. La moyenne des mesures induit souvent une erreur d’analyse des données, dont les conséquences peuvent être fâcheuses en termes de décision.
Un autre exemple d’erreur de jugement
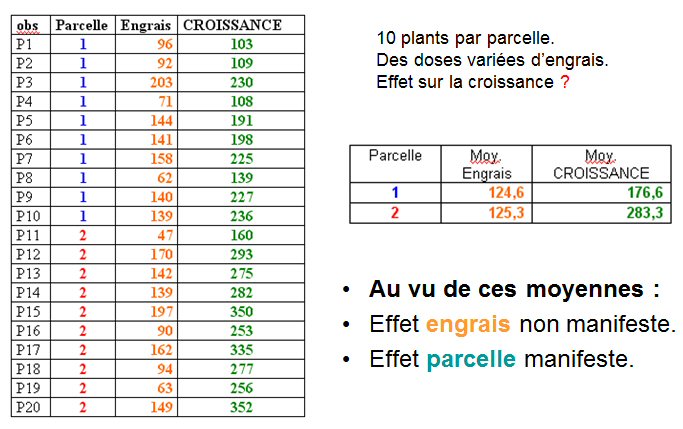
Pour éviter le recours à la moyenne, et coller de plus près à la réalité des mesures, traçons l’ensemble des valeurs brutes des trois variables, rangées, par exemple, par parcelles (figure 1) :
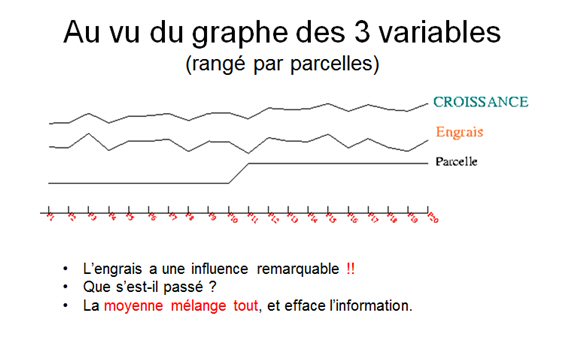
Et voici les mêmes données rangées dans un autre ordre (figure 2) :
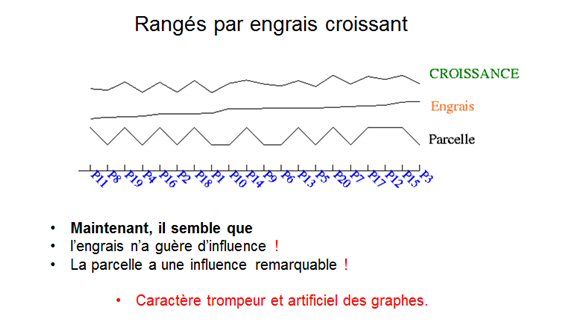
Selon l’ordre de représentation des trois variables, le « ressenti » visuel est différent. L’ordre adopté dans la figure 1 n’est pas plus légitime que l’ordre adopté dans la figure 2. Or il y a encore bien d’autres façons de ranger les 20 observations, tout en conservant la simultanéité des trois variables. "On doit savoir que pour découvrir l'ordre, il faut y travailler avec beaucoup d'application" (Descartes, Regulae XIV).
D’où la nécessité d’une représentation objective :
Une représentation sans ordre préfiguré
L’ordre dans lequel sont rangées les observations n’intervient pas dans le calcul du coefficient de corrélation. Il n’y a donc pas d’axe de coordonnées en Iconographie des Corrélations (quel que soit le nombre de variables considérées).
Appliquons l’iconographie des corrélations à notre tableau de données (figure 3) :
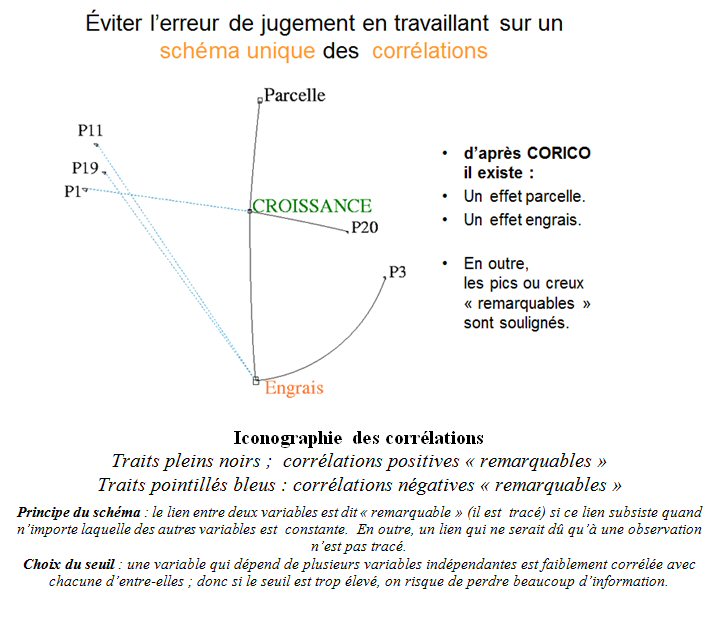
L’iconographie des corrélations met en évidence, sur un schéma global, unique et cohérent, les influences (indépendantes entre-elles) de l’engrais et de la parcelle sur la croissance de la plante.
Objection
On dira peut-être que l’ensemble des figures 1 et 2 contient toute l’information, et qu’on peut se passer de la figure 3.
Cependant, la démarche consistant à tracer les variables en parallèle selon divers ordres (ici, celui des parcelles, puis celui des engrais croissants) est difficilement généralisable, car
Conclusion générale
Pour éviter l’erreur induite par la moyenne, mieux vaut, dans la mesure du possible, s’appuyer sur les données brutes. Mais comment faire parler ces chiffres sans introduire un biais d’interprétation ? Un bon moyen est l’iconographie des corrélations.
L’iconographie des corrélations (figure 3), condense l’essentiel sans recourir à la moyenne et sans privilégier un ordre préétabli, conformément à la troisième règle du Discours de la méthode qui "suppose même de l'ordre entre ceux qui ne se précèdent point naturellement les uns les autres." (Descartes).
La méthode revient à dégager délicatement l’évidence de sa gangue de redondances. Nul besoin d’organiser ce qui s’organise tout seul.
Ce schéma visuel et intuitif, non passé par le prisme des souvenirs parasites et des idées préconçues, ne suppose pas une fonction linéaire du temps, ou d’une quelconque variable. Il épouse la réalité des données disponibles, et nous permet de prendre du recul.
Indépendant de nos attentes, il favorise l’attention à toutes les interdépendances. Nous retrouvons cette capacité d’étonnement, qui seule permet les découvertes.
D’où vient l’incertitude ? Du nombre de causes de variations possibles (facteurs de confusion).
L’iconographie des corrélations est un outil d’autant plus sûr qu’on travaille directement sur les données brutes, et qu’on dispose de plus de variables en rapport avec la question. C’est aussi un moyen d’éliminer les « fausses bonnes corrélations ».
Voir aussi :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.