Décomposition fine des séries temporelles avec CORICO
Une méthode souple et générale n'exigeant ni un échantillonnage régulier, ni des séries stationnaires.
Le logiciel de série temporelle ou série chronologique CORICO allie une grande convivialité à une finesse d’analyse inégalée.
8 bonnes raison d'adopter CORICO séries temporelles
Le logiciel
Exemple: décomposition du trafic autoroutier ...
Décomposition du trafic autoroutier
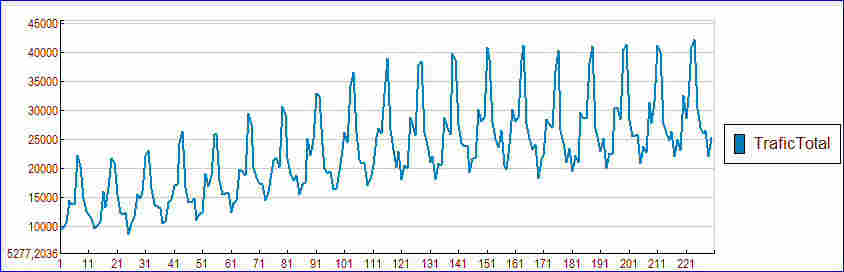
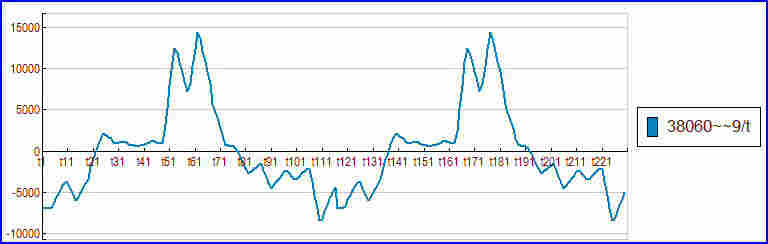
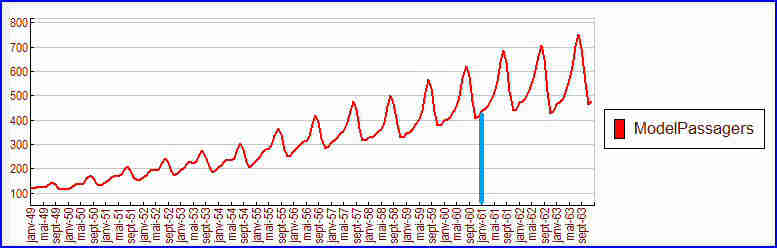
Une série temporelle : le trafic autoroutier en France durant 230 mois de la fin du XX ème siècle :
Voici le modèle obtenu par CORICO, et son résidu :
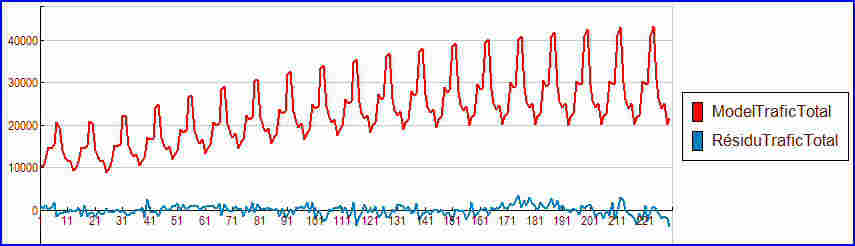
Ce modèle est la somme de trois composantes :
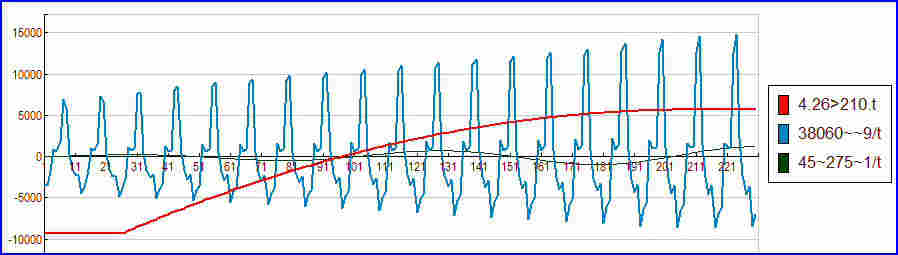
Muni de ce modèle, il est possible de prédire l'évolution ultérieure du trafic.
Voici le détail du motif périodique sur deux années successives. Il reflète les périodes de pointes et les creux de trafic. Il n'y aurait aucun intérêt, pour la compréhension physique, de le décomposer lui-même en une somme de sinusoïdes.
Une avancée majeure dans la décomposition et la prévision des séries temporelles ...
Une avancée majeure dans la décomposition et la prévision des séries temporelles.
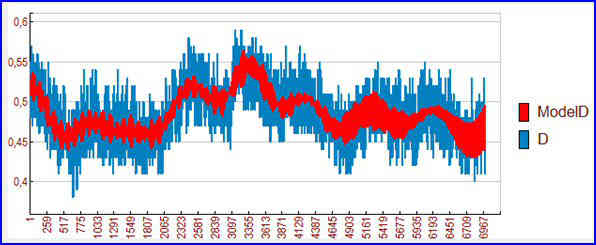
Par rapport aux méthodes classiques (telles que moyennes mobiles, processus gaussiens, ARMA, ARIMA, Markov ou Box-Jenkins, calcul différentiel, analyse de Fourrier, dispersion de phase, ondelettes, spline, EMD...), la méthode CORICO, simple dans son emploi et précise dans ses résultats, bien adaptée à la prévision, permet un calcul rigoureux même lorsque la cadence d'échantillonnage n'est pas régulière.
L'approche classique des séries chronologiques consiste à décomposer la série temporelle en une tendance,une composante saisonnière et une composante aléatoire. Mais la réalité est souvent plus complexe : plusieurs tendances et plusieurs saisonnalités se combinent presque toujours!
Voyons les forces et les faiblesses des différentes approches.
Inconvénient : la forme et la longueur de la fenêtre sont fixées au début de l’analyse, ce qui suppose une connaissance a priori du phénomène.
Cependant, pas plus que la STFT, cette méthode n’est adaptée aux signaux non stationnaires et non linéaires dont on ne connaît pas a priori les caractéristiques. Les ondelettes sont utiles pour le débruitage, l’analyse d’image et la compression de données, mais ne se prêtent pas à l’extrapolation et à la prédiction des séries temporelles.
L’extraction des modes ou IMF est une opération non linéaire, mais leur recomposition est linéaire.
En revanche, l’EMD ne détectera pas une composante non oscillante (par exemple, une fonction croissante ou en marche d’escalier, etc.). De plus l’usage des maxima ou minima locaux la rend très sensible à l’échantillonnage.
La méthode CORICO, au contraire, à la fois descriptive et prédictive, ne repose sur aucune hypothèse, si ce n'est sur l'idée que le futur ressemble parfois au passé. L’une des forces du logiciel CORICO repose sur la distinction automatique des événements exceptionnels d’avec ceux susceptibles de se reproduire.
CORICO décèle et démêle dans les séries temporelles les interférences de divers cycles et saisonnalités avec des ruptures de tendances en " marches d'escaliers ", en " V ", des " ruptures logistiques ", des motifs périodiques, et des événements accidentels tels que des pics isolés ou des " morceaux d'ondes ". Le logiciel détecte aussi les variations au cours du temps de l’amplitude d’une oscillation.
Muni d'une prévision fiable, vous pouvez appuyer vos décisions et procéder à des corrections.
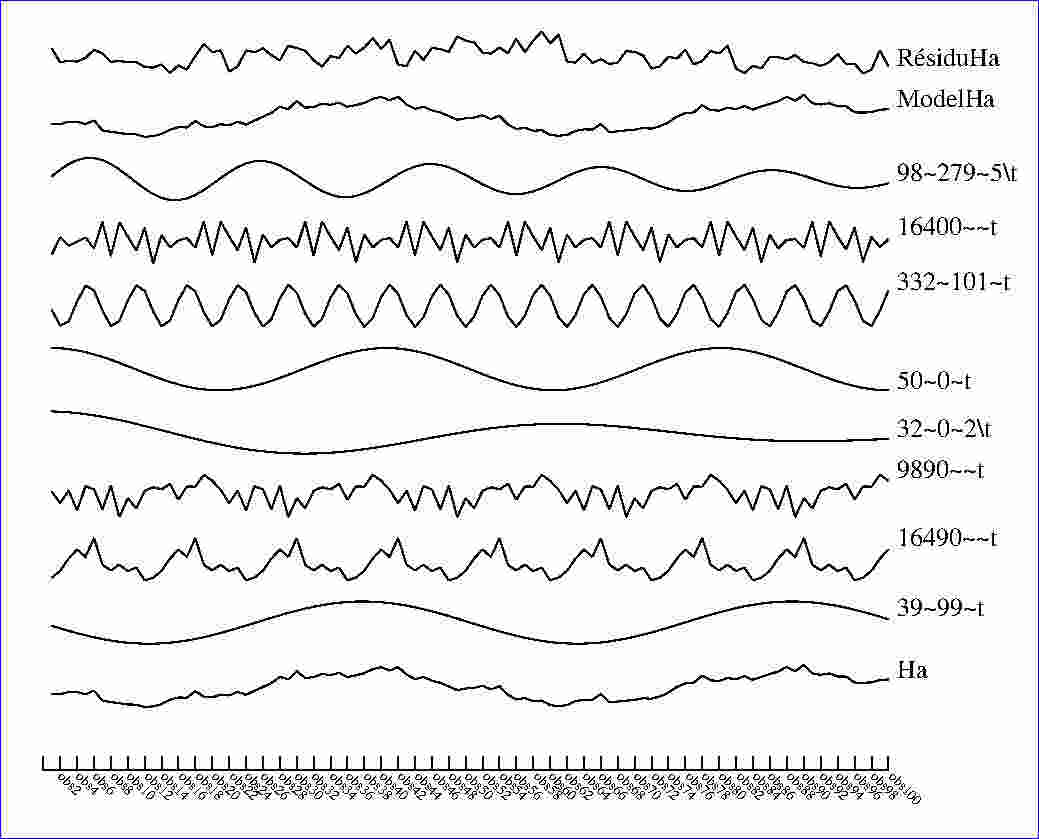
Dans la figure ci-dessus, CORICO a détecté 8 composantes de la série temporelle Ha, à savoir 5 composantes sinusoïdales, et 3 motifs périodiques non sinusoïdaux (16490~~t, 9890~~t, 16400~~t). ModelHa, qui est la reconstitution de la série au moyen de ces 8 composantes, permet la prévision en fonction du temps t.
Un autre exemple : le trafic aérien ...
Un autre série temporelle : le trafic aérien
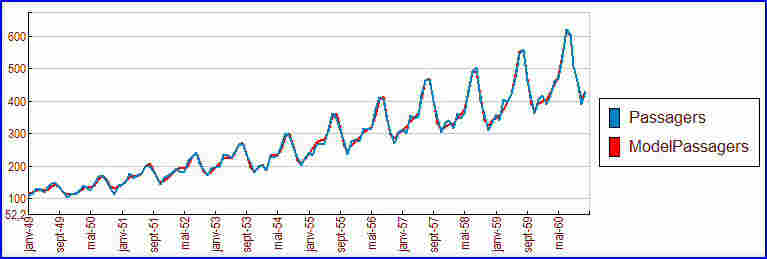
L’exemple du trafic aérien international est souvent cité pour comparer des logiciels de séries temporelles :
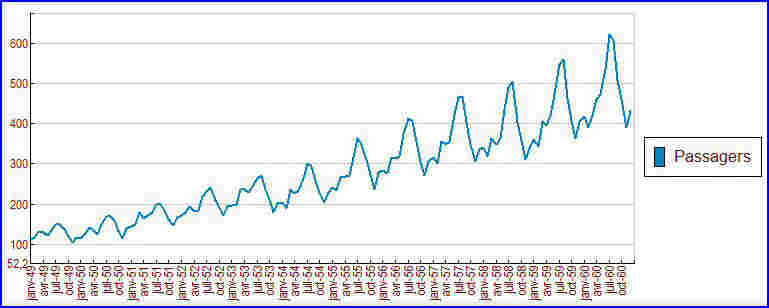
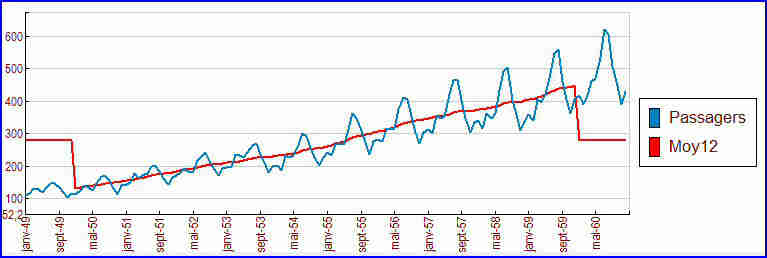
Le nombre de passagers augmente régulièrement. Là-dessus se superpose une variation cyclique annuelle. Ces variations à l'intérieur d'une même année sont de plus en plus fortes.
Une moyenne mobile d’ordre 12 (c’est à dire sur les 12 points précédents et suivants) permet de lisser les données en filtrant les cycles annuels, mais elle induit un effet de bord à droite et à gauche de la courbe, où elle ne peut être calculée :
Une autre méthode, le lissage exponentiel simple, qui est une moyenne pondérée sur les valeurs passées, n’a pas d’effet de bord, il exige cependant le choix subjectif d’un paramètre béta, fixant l’influence plus ou moins grande du passé. Ci-dessous, béta = 0.9 :
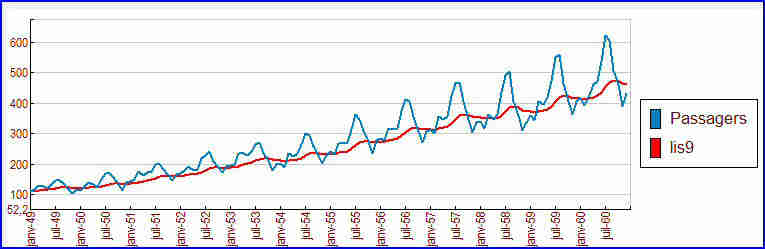
Ce lissage est optimal pour des séries temporelles sans tendances ni saisonnalité. On peut l’améliorer avec le lissage exponentiel double ou, mieux, avec le lissage exponentiel triple ou de Holt-Winters. Ce dernier requiert de fixer a priori trois paramètres, dont la période attendue de la saisonnalité.
Outre le choix toujours subjectif des paramètres, cette méthode ne permet pas de décomposer une série comportant plusieurs cycles et plusieurs tendances superposés.
Nous allons donc utiliser une autre méthode, plus simple, plus précise et plus générale, puisqu’elle ne requiert aucun paramètre et permet la décomposition complète de la série temporelle.
Le modèle de régression non postulé, trouvé par le logiciel CORICO, est le suivant :

Le sens des noms des prédicteurs de cette équation de régression, propre au logiciel, sera mieux compris graphiquement :
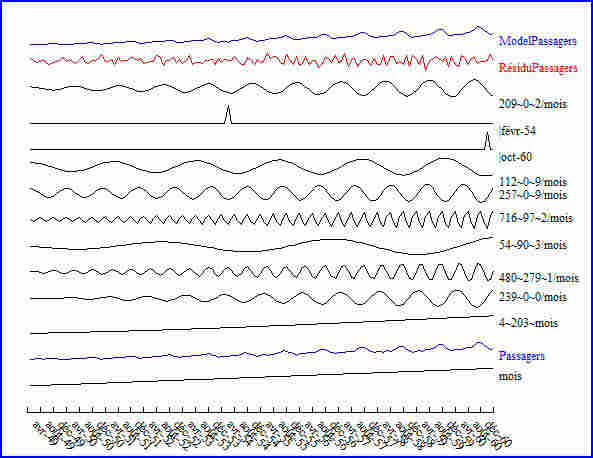
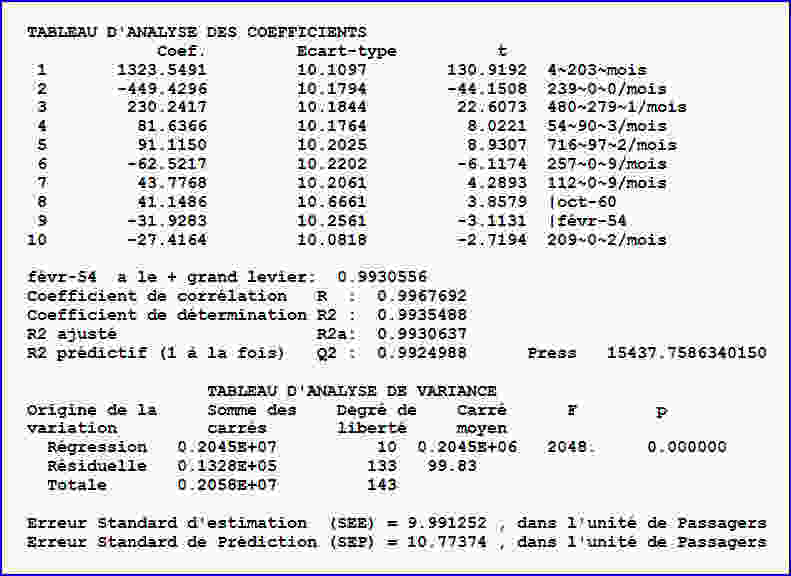
Le tableau ci-dessous donne le détail des coefficients, les périodes en mois, et les points atypiques.
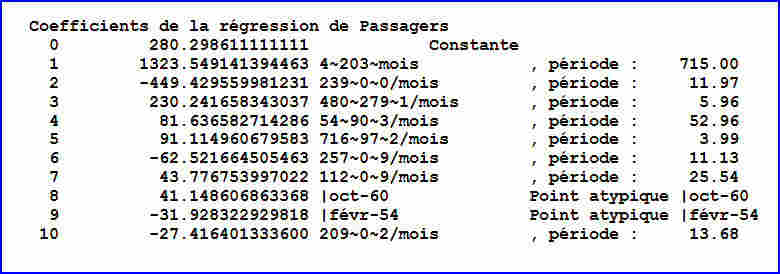
Comme les prédicteurs sont classés par ordre d’importance décroissante, on voit tout de suite, d’après les coefficients, que les trois premiers prédicteurs expliquent presque toute la variabilité.
A titre indicatif, le logiciel fournit aussi ci-dessous le tableau d’analyse des coefficients et le tableau d’analyse de variance.
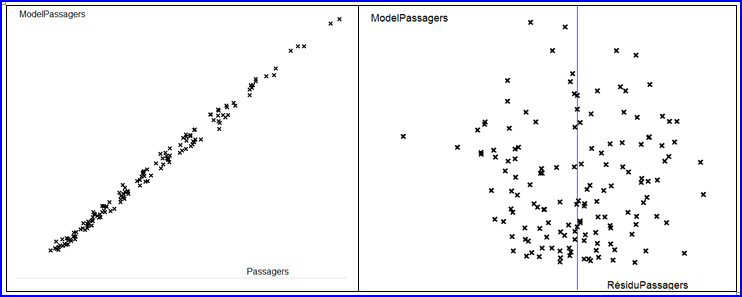
Les graphes ci-dessous représentent, à gauche le modèle des Passagers en fonction des Passagers, et à droite les résidus correspondants. C’est un bruit aléatoire totalement sans structure (« bruit blanc ») :
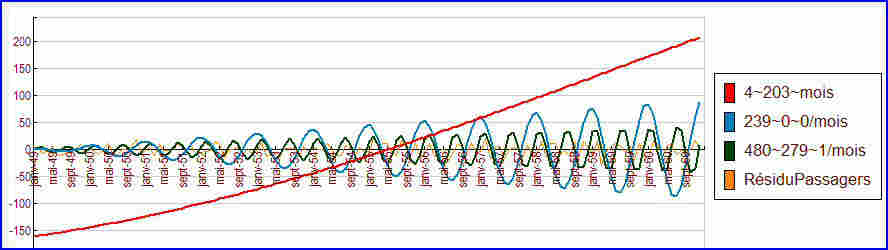
Le graphe ci-dessous montre, par rapport à l’amplitude du premier prédicteur (la tendance, en rouge), les amplitudes relatives du deuxième prédicteur (en bleu, de période annuelle), du troisième prédicteur (en vert, de période semestrielle), et enfin du résidu.
Ainsi l’interprétation est simple avec le logiciel CORICO : Il n’est pas besoin d’examiner un autocorrélogramme ou un périodogramme. Le calcul est d’autant plus précis qu’il n’est pas fondé sur des moyennes mobiles (en effet le choix de l’ordre de la moyenne mobile est toujours délicat : des saisonnalités parasites peuvent apparaître).
Muni de ce modèle nous pouvons calculer une prédiction du trafic, par exemple pour les 3 années suivantes (au-delà du trait bleu) :
Prise en compte d’influences diverses ...
Prise en compte d’influences diverses
L’analyse d’une série temporelle sera meilleure si l’on tient compte des événements qui ont pu influencer la série (changements législatifs ou économiques, accidents majeurs, grèves, données climatiques, etc.)
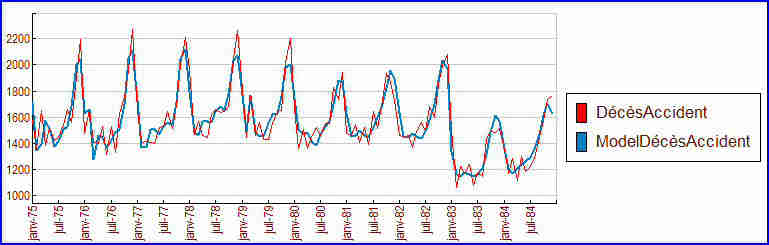
Exemple : le nombre de décès par accident tous les mois sur les routes d’Angleterre, de janvier 1975 à décembre 1984, présente l’allure suivante :
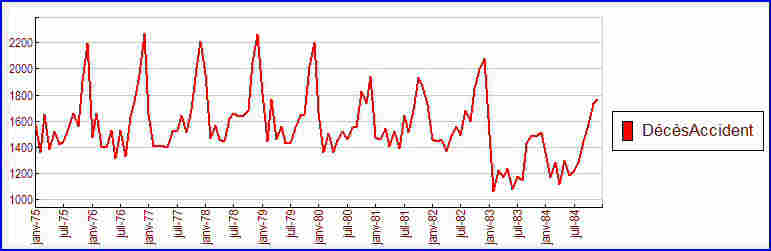
En janvier 1983, le port de la ceinture a été rendu obligatoire pour les automobilistes anglais (Seat Belt Law). Deux cas sont possibles :
Soupçonnant l’influence de l’obligation du port de la ceinture sur la réduction du nombre de décès, l’analyste ajoute à ses données une variable « SeatBeltLaw » qui vaut 0 avant janvier 1983, et qui vaut 1 à partir de janvier 1983.
A partir de là, le logiciel CORICO construit le modèle de régression multiple suivant :

Le sens des noms des prédicteurs, rangés dans l’équation par importance décroissante, sera mieux compris sur le graphe suivant (en bleu, les variables d’entrée) :
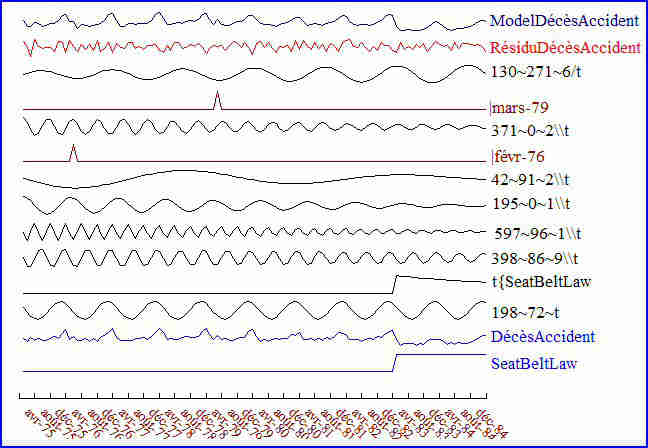
Détail des prédicteurs du modèle :
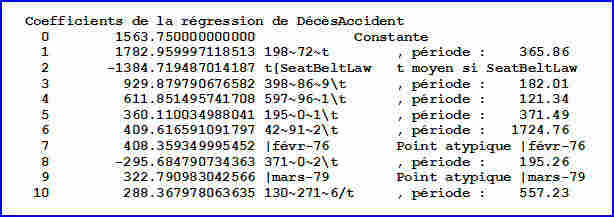
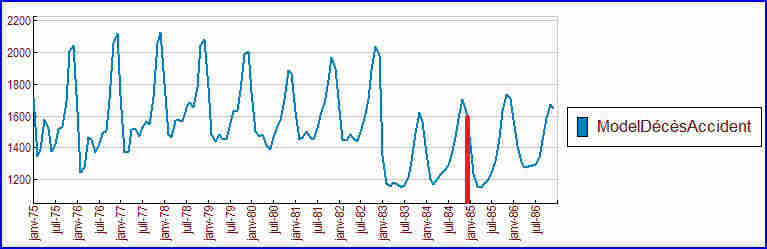
Nous pouvons utiliser l'équation du modèle pour prévoir les décès sur les années suivantes, à partir d’un fichier de données contenant les temps supérieurs à décembre 1984, et une variable SeatBeltLaw constante = 1. Prévision au-delà du trait rouge (janvier 1985) :
2 – L’analyste ne connaît pas l’existence de la « Seat Belt Law »
Dans ce cas, le logiciel CORICO donne le modèle de régression suivant, fondé seulement sur des fonctions du temps :

Le R2ajusté est légèrement moins bon que celui du modèle précédent. En effet le logiciel CORICO a dû trouver automatiquement l’existence d’une rupture en janvier 1983, notée 4.96>98.t. Les modèles sont cependant très semblables, ce qui montre la robustesse de l’algorithme. Toutefois la décroissance de l’influence de la loi SeatBeltLaw au cours du temps n’est plus perçue dans ce modèle :
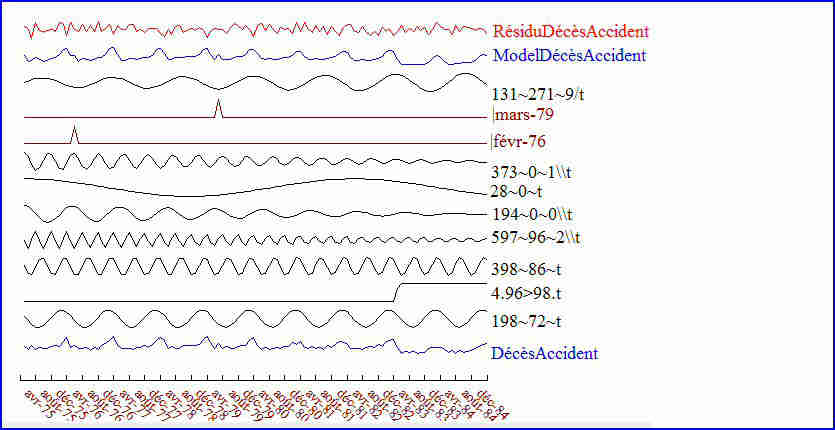
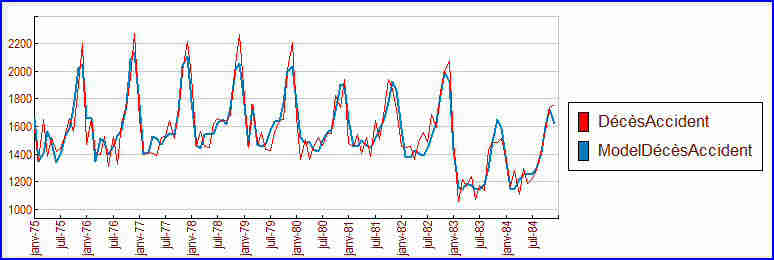
L’ajustement semble presque identique à celui du modèle précédent, mais la prévision sur les deux années suivantes est légèrement différente, puisqu’on dispose d’un peu moins d’information. Prévision au-delà du trait orange (janvier 1985):
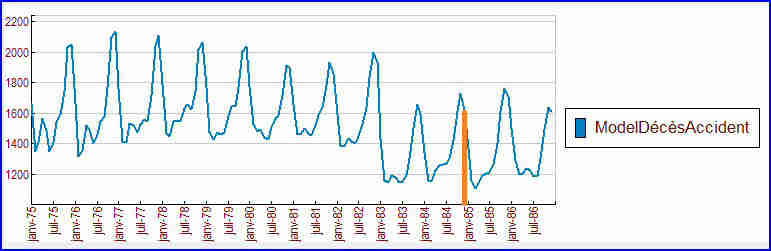
En conclusion, le logiciel CORICO permet de tirer le meilleur parti de l’information disponible. Bien sûr, il est toujours préférable, lorsqu'on les connaît, de tenir compte des événements qui peuvent influencer la série étudiée.
Cas de l'échantillonage irrégulier ...
Echantillonnage irrégulier dans le temps
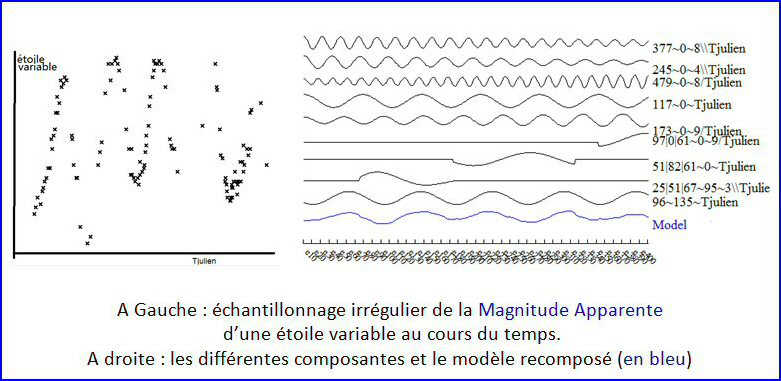
Les séries chronologiques d’échantillonnage irrégulier se rencontrent dans de nombreux domaines industriels et scientifiques :
L’approche courante consiste à transformer l’échantillonnage irrégulier des données en observations également espacées, par interpolation - le plus souvent linéaire - puis d'appliquer les méthodes classiques. Malheureusement la transformation des données introduit des biais difficiles à quantifier, surtout si l'écartement des observations est très irrégulier.
Au contraire, CORICO permet d’analyser une série inégalement espacée dans le temps sous sa forme non modifiée, évitant ainsi les biais d’interpolation lors du calcul du modèle.
Le modèle une fois connu, on en déduit les valeurs non échantillonnées.
Champ d'application des séries temporelles
Les séries temporelles ou séries chronologiques, c’est-`a-dire les collections de mesures ordonnées dans le temps, sont présentes un peu partout. Leur analyse est requise dans de nombreuses sciences et techniques, généralement pour comprendre une évolution passée et pour prévoir un comportement futur. La prévision consiste à estimer une observation future à partir de la connaissance historique.
En l’absence de recherche de variables explicatives, l’accent est mis sur les séries univariées. Dans le cas contraire, par exemple en économie et finance, les dépendances entre séries peuvent faciliter des décisions d’arbitrage. Il convient alors de considérer des séries multivariées .
On trouve des exemples de séries chronologiques univariées dans de très nombreux domaines :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.
Economisez des années en Recherche et Développement :
INDUSTRIE - RECHERCHE - QUALITÉ - ÉPIDÉMIOLOGIE - ENQUÊTES - ECONOMETRIE ...
FORMATION
- Découvrir et maîtriser
- l'Analyse de Donnéees
- le Plan d'expériences
- les Séries Temporelles
- Voir les formations