Une représentation réellement multidimensionnelle
Une réflexion sur la représentation et la visualisation multidimensionnelle, nous conduit à adopter une nouvelle méthode : « l’iconographie des corrélations ». Exemple :
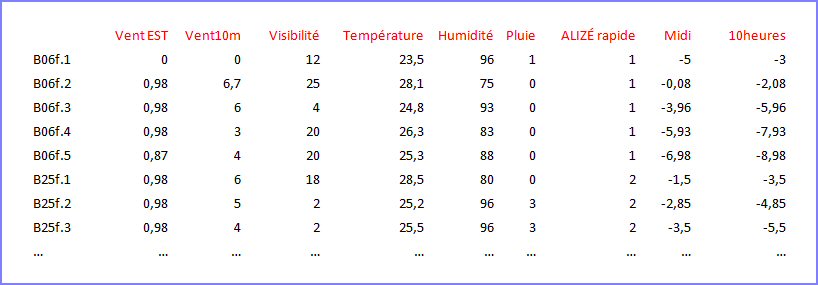
Ce tableau, qui comprend 9 colonnes et 54 lignes, est extrait d’un tableau comportant beaucoup de variables mesurées à Kourou en Guyane de février à mars. Une seule variable est qualitative (Alizé rapide) mais il pourrait y en avoir beaucoup plus. Nous ne conservons que 9 variables pour mieux dégager la difficulté :
Comparons quelques représentations traditionnelles (figures 1 à 4) à l' "iconographie des corrélations" (figure 5).
1 - Représentation bidimensionnelle
Représentons, en fonction du vent à 10m du sol, les 8 autres paramètres :
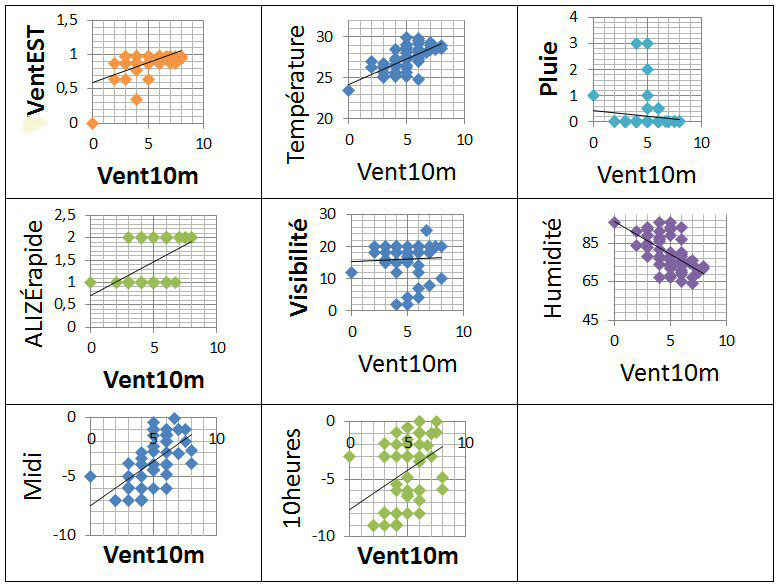
Figure 1
Quelle sont les variables qui influencent le plus (ou sont le plus influencées par) le vent à 10 m du sol ?
La température semble fortement corrélée à la force du vent à 10 m, mais l’humidité aussi, de même que la variable « Midi ».
Au vu des 8 dessins, il est difficile de répondre avec certitude, d’autant que les 8 variables sont elles-mêmes liées entre elles. Il faudrait représenter les 36 couples possibles de variables. Comment en faire la synthèse?
Quand bien même nous y consacrerions du temps, l’interprétation risque de dépendre de l’ordre dans lequel les 36 figures auront été examinées.
Lorsque nous considérons la matrice des 36 coefficients de corrélation, le problème demeure :

Submergés par les chiffres, nous avons du mal à en tirer des conclusions assurées.
Le chiffre le plus fort (-0.86) est la corrélation négative entre l’humidité et la température. Mais que dire des autres chiffres ?
Il est difficile de les comparer : une corrélation faible ne signifie pas forcément une faible influence.
En effet, lorsqu’une variable dépend de plusieurs paramètres indépendants, il est normal que sa corrélation avec chacun d’entre eux puisse être faible.
2 - Représentation en fonction du temps
Voici une autre façon de représenter les même données, en fonction du temps :
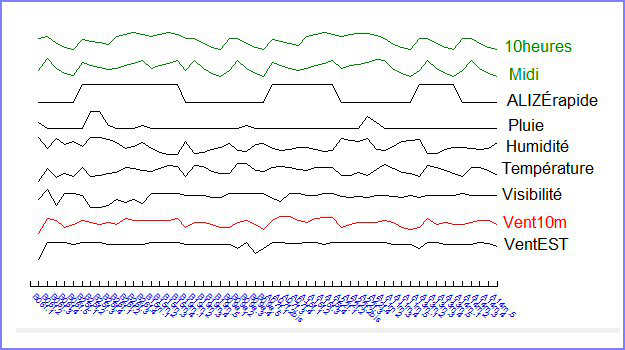
Figure 2 : représentation simultanée des neufs variables en fonction du temps.
La figure 2 est plus globale que la figure 1 : toutes les variables peuvent être comparées deux à deux. Elle est aussi plus complète. Par exemple, nous voyons les 54 valeurs de la variable ALIZÉ rapide, alors que, sur la figure 1, seuls 14 points sont visibles, car plusieurs se superposent.
Malgré tout, il n’est pas facile de départager les paramètres qui ont un effet sur la vitesse du vent à 10 m du sol.
Essayons différentes méthodes de représentation multidimensionnelle :
3 - Analyse en composante principale (ACP)
L’ACP est une méthode classique d’analyse de données multidimensionnelles qui consiste à projeter un nuage de points à N dimensions dans un ou plusieurs plans.
Le premier plan est défini par les deux axes qui expliquent le mieux la variabilité des données, c’est-à-dire dans lequel le nuage projeté s’étale le mieux.
C’est donc au final une représentation bidimensionnelle.
La figure 3 montre le plan défini par les axes 1 et 2 :

Figure 3
Dans ce plan, les variables proches du Vent10m sont VentEST, ALIZÉrapide, 10heures et Midi.
Toutefois les projections dans le plan peuvent laisser croire à des proximités qui en réalité n’existent pas dans l’espace à N dimensions. Il convient donc de considérer les autres plans.
La figure 4 montre le plan défini par les axes 2 et 3 :

Figure 4
Il conviendrait donc d’approfondir l’analyse en considérant l’axe 4, etc.
Inconvénient de l’ACP :
L’interprétation est aisée si toute l’information est expliquée par les premiers axes. Sinon, le pouvoir de synthèse est inversement proportionnel au nombre d’axes nécessaires.
Alors, essayons autre chose :
4 - L’iconographie des corrélations
L’iconographie des corrélations n'est pas la projection sur un plan, mais un schéma explicatif immédiatement exploitable par le décideur.
L’iconographie des corrélations concentre l’information sur une figure unique. Il n’y a pas d’axe à expliquer. L’interprétation ne repose pas tant sur les positions des points que sur les liens dessinés entre les variables :
Un lien « remarquable » entre deux variables est un lien qui ne peut être expliqué par une tierce variable (le lien persiste même si la tierce variable demeure constante).
La figure 5 donne l’iconographie des corrélations des données précédentes. Elle nous apporte, sous une forme nette, plus d'informations directement exploitables que les figures précédentes :
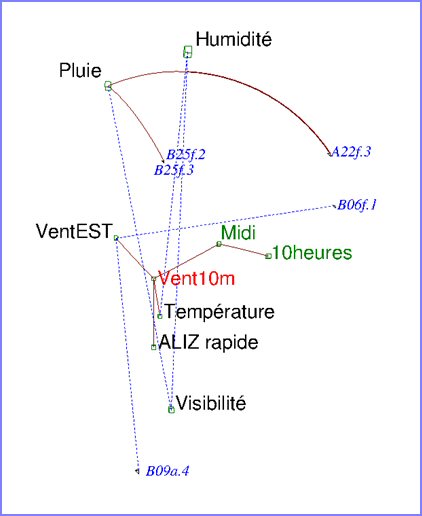
Figure 5 : l'essentiel de la matrice de corrélations
Traits pleins : liens positifs ; pointillés : liens négatifs
Le vent à 10 m du sol est lié par des traits pleins (corrélations positives) à quatre paramètres qui eux-mêmes ne sont pas liés entre eux, à savoir :
. Température
. Vent d’EST
. Alizé rapide
. Midi.
Ainsi le vent à 10 m augmente quand la température augmente, et il augmente aussi plutôt à midi qu’à 10 heures (sans doute un effet de brise de mer). Mais la température n’augmente pas forcément à midi (absence de lien direct).
Le vent à 10 m est plus fort par vent d’EST, et en période d’Alizé rapide, mais ces deux dernières variables ne sont pas liées, comme on le vérifie sur les courbes temporelles de la figure 2. Pourtant ces deux variables semblaient proche dans les deux premiers plans de l'ACP.
La figure 5 montre trois pics de pluie remarquables : B25f2, b25f3 et A22f3 (c'est-à-dire 25 février 2ème et 3ème mesures, et 22 février 3ème mesure). Ces pics, sont visibles sur les courbes temporelles de la figure 2. En revanche, l’ACP est moins claire en ce qui concerne A22f3.
Afin d'alléger la figure, seuls sont tracés les pics qui font l’objet d’un lien « remarquable ».
Les traits pointillés de la figure 5 indiquent une baisse de température et de visibilité lorsque l’humidité ou la pluie sont fortes. Cette opposition, facile à expliquer physiquement, apparait dans l’ACP, bien que moins nettement.
Conclusion de la visualisation
L’iconographie des corrélations montre nettement l’essentiel en une seule figure, quelle que soit la dimension des données.
Les liens « remarquables » sont tracés s’ils vérifient une série sévère de tests simples (à savoir : la corrélation subsiste même si l'on maintient constante n'importe laquelle des autres variables).
Aussi l’utilisateur peut s’appuyer sur eux avec assurance dans l’interprétation des données.
Lorsqu’on analyse un tableau plus complet, avec variables quantitatives et qualitatives, l'interprétation d'une ACP est encore plus délicate. Au contraire l’interprétation de l'Iconographie des corrélation est
Dans la figure 6, on retrouve sans peine les informations déjà présentes dans la figure 5 ; mais encore beaucoup d'autres informations utiles :
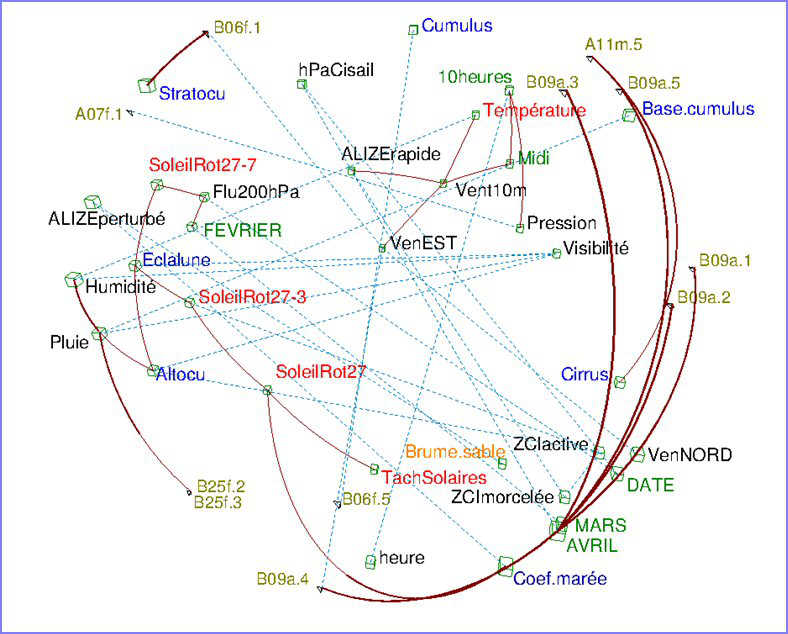
Figure 6 : une visualisation réellement multidimensionnelle
Disposant de plus d’informations, il est possible de lever bien des doutes. Aussi est-il recommandé de travailler d’emblée sur l’ensemble des variables disponibles.
Une absence de lien avec telle ou telle variable peut être une information aussi intéressante que la présence d’un lien.
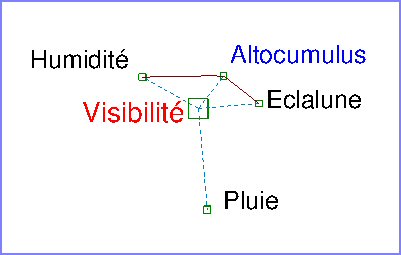
Figure 7
Une fois l’analyse réalisée sur l’ensemble des variables, il est possible de ne tracer qu’une partie des éléments du dessin, pour clarifier la figure.
Par exemple, on peut ne tracer que les liens à la visibilité.
La figure 7 lève un doute, car on pouvait se demander, dans la figure 6, si le lien entre humidité et altocumulus passait ou non par la pluie (ce n’est pas le cas).
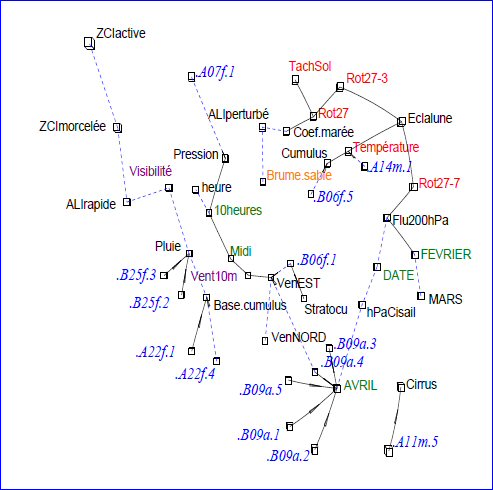
Figure 8
Mais ce n'est pas tout.
L'influence de l'humidité sur la visibilité est évidente.
On peut souhaiter s'en affranchir, c'est à dire tracer la figure des liens à humidité constante.
Alors la figure 6 se transforme en la figure 8.
Certains liens ont disparu. D'autres sont apparus.
Par exemple, une fois l'influence de l'humidité retirée, il apparaît que la visibilité est liée négativement (pointillés) à l'alizé rapide. Donc, en présence d'alizé rapide la visibilité tend à diminuer, toutes choses égales par ailleurs.
Sur la figure 8, la position des points a été optimisée pour limiter la longueur des traits pointillés, et ainsi clarifier la figure.
On peut aussi, pour clarifier une figure, ne tracer que les variables, et pas les instants d’observation...
Méthode purement géométrique, accessible à tous, l’iconographie des corrélations n’exige pas de connaissances en statistique, et s’apparente à la perception visuelle intuitive.
D’une grande précision, car elle subordonne l’interprétation à une vue complète et non redondante des faits disponibles, elle ne repose sur aucune hypothèse.
Ne pas confondre ce qui est distinct, ne pas distinguer ce qui est confondu, empêche d’errer sur de fausses pistes, et nous épargne beaucoup de temps perdu.
La méthode permet de « déchiffrer », au sens propre, les données ; mais, bien sûr, c’est à l’utilisateur d’en découvrir « le sens », ce qui lui sera d’autant plus facile qu’il est familier avec la matière sur laquelle porte l’analyse.
En résumé
La représentation multidimensionnelle par iconographie des corrélations est
En outre, grâce aux « corrélations partielles (voir bibliographie) c’est un outil expérimental puissant lorsqu’on ne peut fixer les conditions de l’expérience.
Voir aussi :