S’affranchir des erreurs systématiques dans le réglage des instruments de mesure, en analyse multivariée.
La « barre d’erreur » autour d’un résultat de mesure traduit une dispersion des résultats, qui n’est pas forcément une « erreur », mais résulte le plus souvent de l’effet naturel du contexte environnant.
Par suite, la manière dont on analyse un ensemble de données peut aboutir à une conclusion ou à la conclusion opposée (paradoxe de Simpson -Yule) !
Appréhender l’effet d'un facteur implique de s’affranchir d’abord des erreurs systématiques, ou, plus exactement, des « effets » systématiques induits, par exemple, par les appareils, les opérateurs, divers laboratoires, etc. Ces facteurs, souvent qualitatifs, introduisent un décalage constant dans la mesure.
L’« Iconographie des corrélations » permet d’éviter que ce décalage, un mauvais réglage de l'instrument de mesure, ou un facteur de confusion, ne se répercute sur l’interprétation des résultats.
La force de la méthode CORICO vient de ce qu’il n’est pas nécessaire de connaître la nature ni la grandeur de ces « effets systématiques » pour s’en affranchir.
Exemple d'erreurs de réglages
Une série d’environ un millier d’essais industriels est réalisée, et plusieurs paramètres sont mesurés, en vue de connaître leurs relations respectives.
Cependant, au cours des essais, les machines ont dû être onze fois démontées. Chaque fois, le réglage a dû être refait.
Une Iconographie des Corrélations est réalisée (figure 1), qui montre une forte influence des montages :
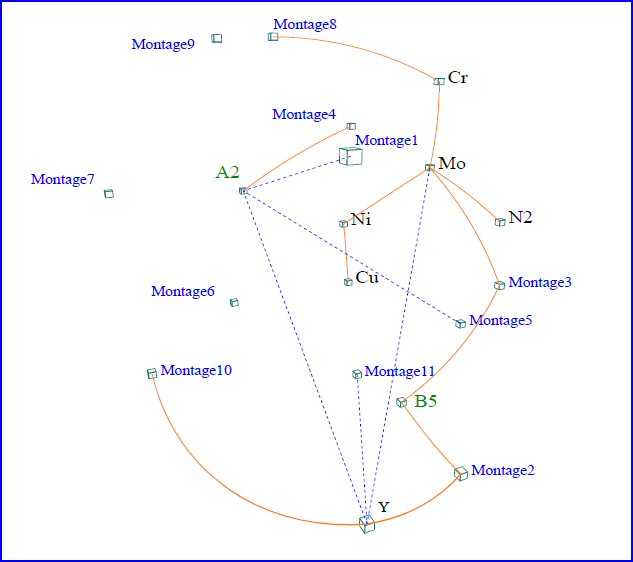
Figure 1 : Iconographie des corrélations au seuil 0.3
Traits pleins : corrélations positives « remarquables »
Traits pointillés : corrélations négatives « remarquables »
Principe du schéma : le lien entre deux variables est dit "remarquable" (il est tracé) si ce lien subsiste lorsque n’importe quelle des autres variables est constante. En outre, un lien qui ne serait dû qu’à une observation n’est pas tracé.
On aurait bien voulu n’avoir pas de lien entre les montages et les autres variables. Or la figure montre, entre autres choses :
Cette influence prépondérante du montage est préoccupante, d’autant que l’industriel s’étonne du lien négatif (pointillé) entre A2 et Y, qu’il trouve absurde.
Les essais sont-ils ratés à cause des multiples démontages ?
Pour élucider cette question, l’industriel demande de tracer Y en fonction de A2, et Y en fonction de B5 (figure 2) :
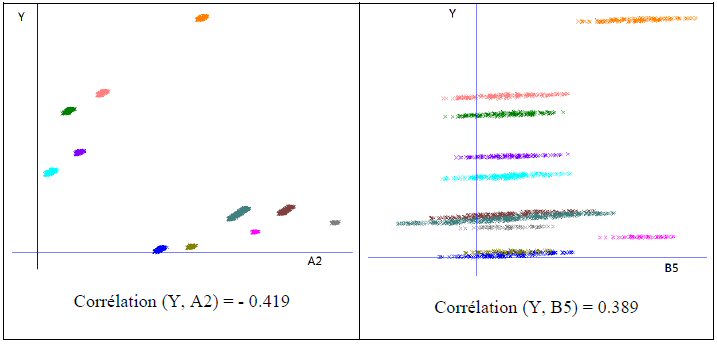
Figure 2 : Y en fonction de A2, et Y en fonction de B5
Les couleurs caractérisent les différents montages.
La figure 2 confirme l’influence des montages, et semble invalider les essais.
S’affranchir de l’influence du montage (facteur de confusion)
Que s’est-il passé pendant les montages ? Des pièces de la machine ont-elles été changées ? Des opérateurs différents sont-ils intervenus ? Nous n’en savons rien. Il n'est d'ailleurs pas besoin de considérer séparément les montages : utilisons l'Iconographie des corrélations pour nous affranchir de l’influence du montage (figure 3) :

Cette fois, l’industriel ne trouve pas absurde l’influence positive de A2 et B5 sur Y. Il fait de nouveau tracer Y en fonction de A2, et Y en fonction de B5 (figure 4) :
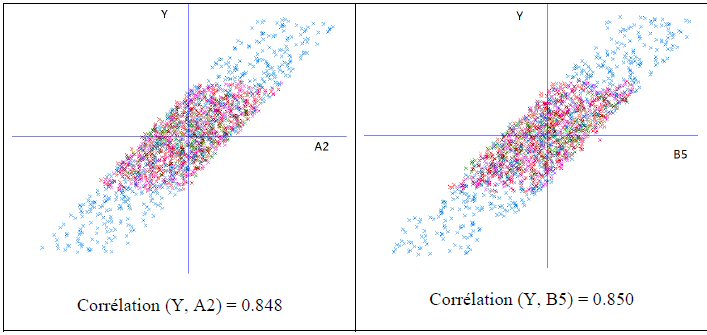
Figure 4 : Y en fonction de A2, et Y en fonction de B5,
après retrait de l’influence des montages
Les couleurs caractérisent les différents montages.
L’iconographie des corrélations a permis de sauver l’interprétation des essais, qui semblait mal partie. Il existe des liens de A2 et B5 avec Y.
Applications
Il est important de connaître les facteurs d’influence pour
La méthode est générale, elle permet aussi de
Voir aussi :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.