Le logiciel CORICO innove dans les modèles de régression linéaire multiple
Un modèle de régression linéaire multiple, facile à appliquer et à expliquer pour le non statisticien, que les données d’entrée soient quantitatives ou qualitatives.
Qu'est-ce que la régression linéaire multiple ?
La "régression linéaire multiple" est une équation donnant la relation entre une variable d'intérêt Y et une ou plusieurs variables explicatives X1, X2, ... :
Y = a + b X1 + c X2 + ...
Par exemple, Y est le GAIN de poids, et les variables explicatives sont le poids initial, les types d'aliments et leur dose, ou des fonctions de ces variables.
Ainsi, le problème de la régression linéaire multiple est triple :
- Choisir les variables explicatives pertinentes, ou des couplages de ces facteurs ("interactions").
- Chercher les coefficients a, b, c, ... correspondants.
- Minimiser les résidus non expliqués ( l’écart entre le modèle et la réalité).
Pour cela, on réalise une série d'expériences avec différentes valeurs des variables explicatives. Le modèle de régression linéaire repose sur la résolution d'un système d'équations où les inconnues sont les coefficients a, b, c, ...
Quatre innovations
CORICO apporte quatre grandes innovations dans la régression multiple :
1 - Gage de simplicité, Vous n'avez pas besoin de postuler a priori la forme du modèle (polynomial ou non) : il est "dirigé par les données".
2 - Une sélection efficace des termes du modèle, classés par importance décroissante parmi des milliers de possibilités, vous permet de travailler même lorsque vos données comportent plus de variables prédictrices que d'observations, ou lorsque ces variables sont corrélées entre-elles.
3 - Les modèles de régression multiple de CORICO sont plus robustes et prédictifs grâce aux "interactions logiques" (influences non linéaires des couplages de paramètres), y compris pour les variables binaires. Vous comprenez mieux les phénomènes sous-jacents et réconciliez vos modèles de régression linéaire multiple avec les données réelles.
Lorsque l’impact d’une variable explicative n’est pas le même dans différents intervalles de valeurs, la méthode se révèle plus souple et plus rapide que la « régression quantile ». Vous n'avez rien à programmer.
4 - Dans le cas de données « longitudinales », c’est à dire mesurées plusieurs fois au cours du temps, CORICO peut détecter des changements structurels : rupture de tendance ou points d’inflexion.
Exemples
1er exemple de régression linéaire multiple
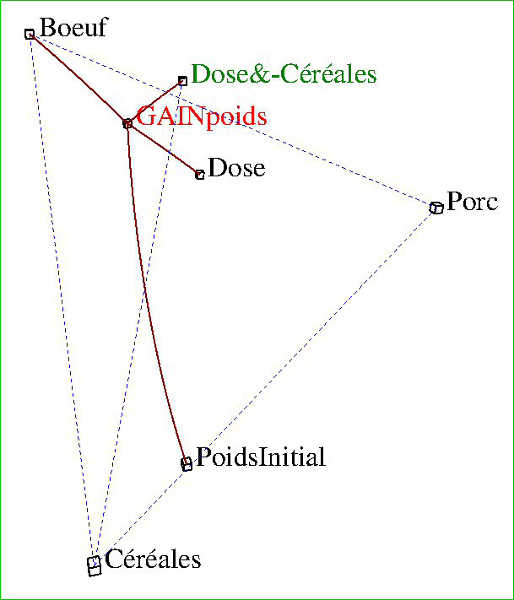
Le modèle polynomial classique à 10 variables explicatives (appelées encore "régresseurs" ou "prédicteurs") donne, pour les données correspondant au "schéma" ci-dessus (R2 ajusté=0.982, F=154, p=0.000000) :

Ce modèle de régression multiple, postulé a priori, est purement analytique (moindres carrés ordinaires) ; il a nécessité10 régresseurs, et il est difficile à interpréter directement.
Le modèle de régression linéaire multiple de CORICO, "dirigé par les données", donne un meilleur R2 ajusté et un meilleur F de Fisher pour 5 variables explicatives seulement (R2 ajusté =0.985, F=370.4, p=0.000000) :

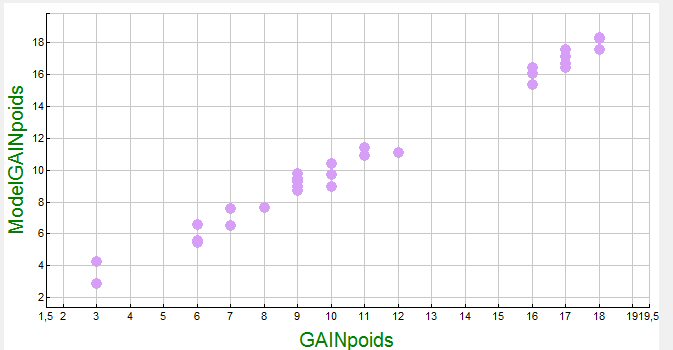
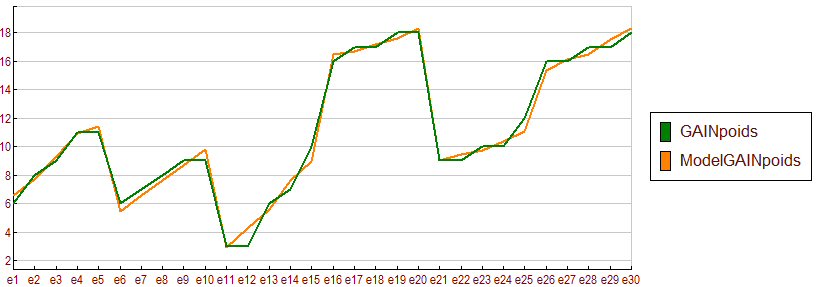
Dans ce modèle de régression multiple (qui n'avait pas été postulé a priori), les variables explicatives sont rangées par ordre d'importance décroissante. Il s'interprète directement, une fois connues les conventions des symboles d'"interactions logiques" (qui ont presque toujours un sens physique) :
Graphe de Pareto
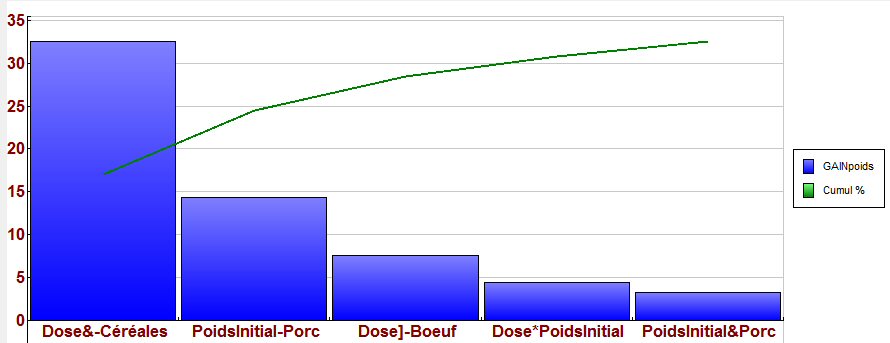
Ce modèle de régression multiple est "parcimonieux" : si l'on ne conserve que les deux premiers prédicteurs, le coefficient F= 219,4 est encore supérieur à celui du modèle polynomial.
Le 2ème modèle a donc plus de chance d'être prédictif pour un nouvel échantillon.
Le solveur de CORICO, est un outil puissant d'optimisation multiobjectif. Vous pouvez indiquer une "désirabilité" sur la ou les réponses (maximiser, ou minimiser ou viser une valeur nominale).
Il vous permet aussi d'introduire dans le modèle de régression linéaire multiple des valeurs à votre choix de Dose, Poids, etc. pour connaître la valeurs correspondante du GAIN de poids.
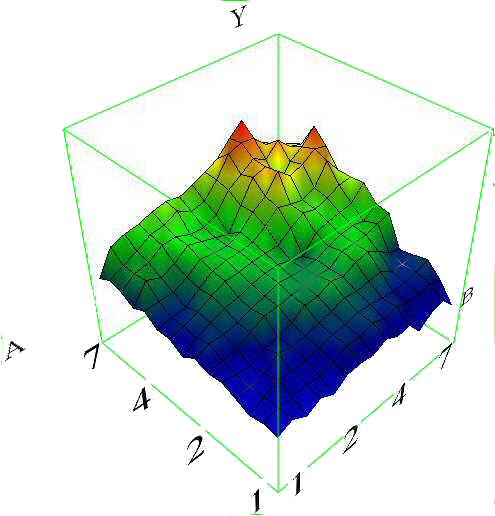
Un industriel souhaite connaître et hiérarchiser les influences éventuelles de 11 facteurs (A, B, C, D, E, F, G, H, I, J, K) sur la performance Y de son procédé de fabrication. Pour cela, il réalise un plan d’expériences de type « Corico » à 25 essais, et 12 niveaux par facteur.
A partir des résultats d’essai, le logiciel CORICO, sans postuler de modèle de régression multiple a priori, obtient l’équation suivante dans laquelle les « interactions logiques » sont rangées par importance décroissante (le nombre de termes de l’équation de régression linéaire multiple est celui qui minimise l’erreur standard de prédiction SEP) :

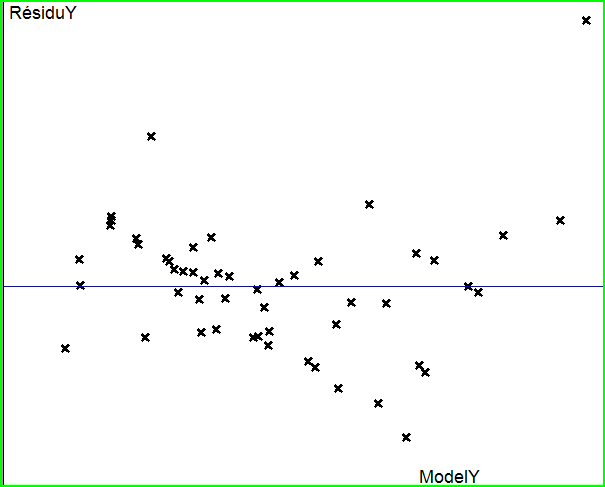
Les résidus sont les écarts entre les valeurs expérimentales et les valeurs restituées par le modèle de régression linéaire multiple.
Les résidus ci-contre sont bien répartis de façon aléatoire.
Ce modèle de régression multiple nous apprend que les seuls facteurs A, B et C parmi les 11, ont de l’importance, et il s’ajuste parfaitement aux données (R2ajusté = 1.0, SEP= 0.4642E-07). « & » signifie « et » ; « # » signifie « varie comme », c’est-à-dire qu’un rapport B/C constant a de l’influence sur Y.
Si, au contraire, le logiciel s’était borné à puiser parmi les seules interactions de type produit, voici l’équation de régression multiple qu’il aurait obtenue :

Cette fois, malgré 9 termes dans l’équation, l’erreur SEP minimum est plus forte que celle de l’équation précédente (R2ajusté = 0.996, SEP= 0.9541E-02). Cette deuxième équation, qui, mathématiquement, s’ajuste encore assez bien aux données, n’a aucun sens physique, car elle attribue de l’influence au facteur H qui cependant n’en a pas. Ici, le modèle de régression multiple, impuissant à expliquer les variations de Y par les seuls facteurs A, B, C et leurs interactions classiques (produits), tente d’ajuster le résidu avec un autre facteur. Il n’aura donc pas une aussi bonne valeur prédictive que le premier modèle.
La méthode automatique de sélection des termes du modèle de régression linéaire multiple (non postulé à priori) vous affranchit des problèmes de multicolinéarité; de plus, comme la méthode PLS (mais de façon bien différente), la méthode CORICO permet de traiter beaucoup de variables même si le nombre d’observations est faible.
Les arbres de classification ou de régression
Parfois aussi appelés arbres de segmentation ou de décision, ils fournissent des modèles à la fois explicatifs et prédictifs. Présentés visuellement sous forme d’arbres, ils offrent également des règles descriptives en langage naturel.
Ils servent à expliquer ou prédire l’appartenance d’objets (observations, individus) à une classe (ou modalité ou catégorie) d’une variable qualitative ou quantitative, à partir de variables explicatives quantitatives et/ou qualitatives.
La méthode CORICO est un moyen d’éviter les modèles de régression multiple qui n’ont aucun pouvoir de prédiction, même s’ils expliquent très bien les résultats de l’étude. Son principe de sélection robuste des termes du modèle est peu sensible à une éventuelle colinéarité entre les variables explicatives, et fonctionne encore si le nombre d'observations est inférieur au nombre de variables explicatives (cas fréquent).
La méthode vous permet aussi de travailler sur de multiples réponses (chacune ayant un modèle différent), pour trouver le meilleur compromis.
D'autres exemples de régression linéaire multiple :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.