Analyse d'un plan de mélange binaire avec CORICO
Dans cet exemple, nous verrons comment analyser un plan de mélange, et comment optimiser la réponse de l'expérience. Trois modèles seront comparés.
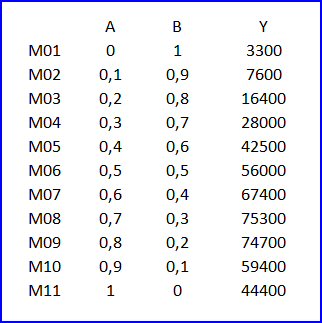
Voici un plan de mélange binaire. C’est le plan de mélange le plus simple, puisqu’il ne contient que deux constituants A et B. Les contraintes sur les proportions du mélange sont :
0 < A < 1
0 < B < 1
A + B = 1
Y est la réponse de l’expérience. On cherche à l’exprimer par un modèle de régression linéaire multiple, en fonction de A et B, afin de pouvoir prédire la réponse pour des expériences non encore réalisées.
Cependant, puisqu’il n’y a que deux constituants, la valeur de B est forcément connue si la valeur de A est donnée. La colonne B est redondante, et nous pouvons chercher une fonction de A seulement.
Il suffit donc ici de fournir au logiciel CORICO un fichier contenant seulement la colonne A et la colonne Y.
Comment le faire avec CORICO ?
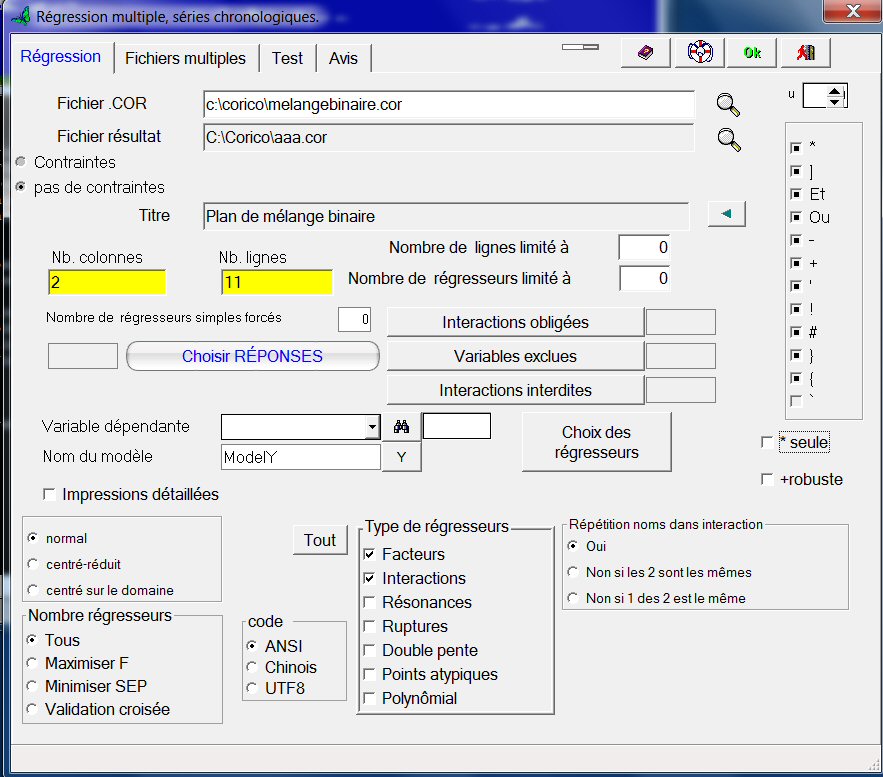
Au menu Outils…Régression multiple, sélectionnons le fichier melangebinaire.cor qui contient le tableau de données.
Par défaut le fichier résultat s’appellera aaa.cor :
Modèle polynomial
Construisons d’abord un modèle polynomial classique. Pour cela, cochons « * seule » afin de désactiver toutes les interactions logiques autres que l’interaction « * » :
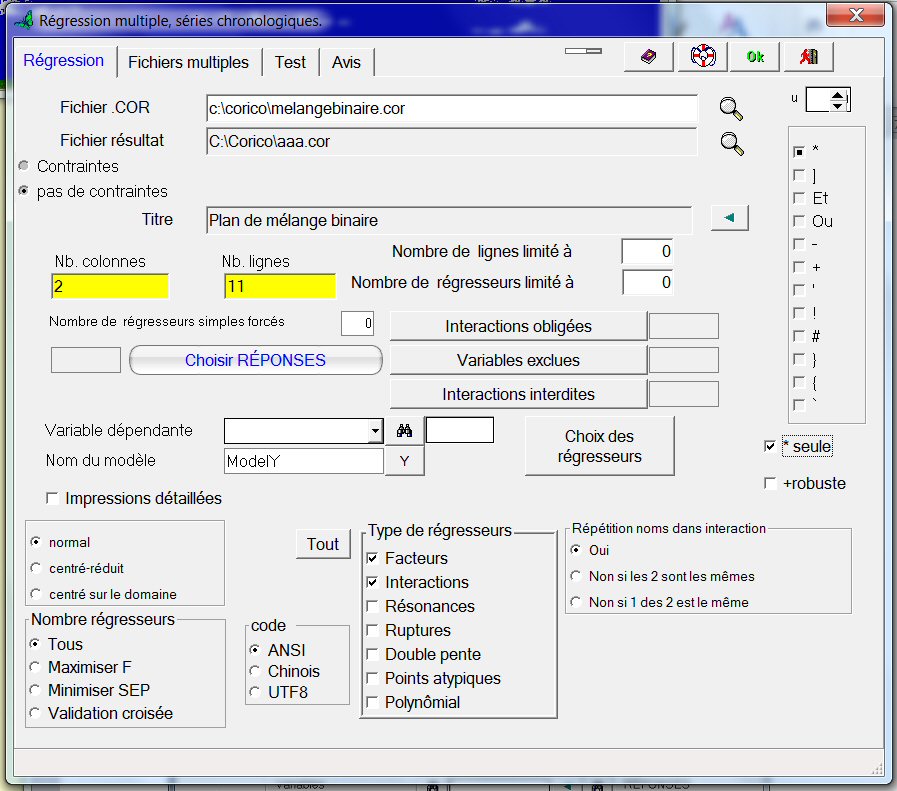
Il suffit maintenant de cliquer sur le bouton « Choisir réponse ». Une fenêtre s’ouvre ; cliquons sur Y, qui passe alors de la colonne de gauche à la colonne « Réponse », à droite :
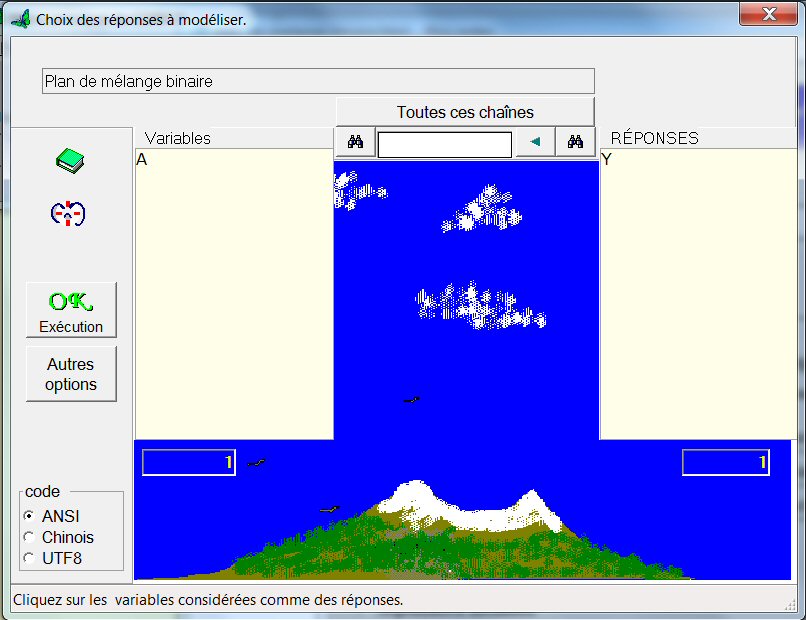
Cliquons sur le bouton « OK Exécution », et le modèle de Y en fonction de A apparaît :

Il s’agit d’un modèle polynomial d’ordre 2. Les coefficients R2ajusté et Q2, permettent respectivement d’évaluer les qualités descriptives et prédictives du modèle. Ils doivent être le plus proches de 1 possible.
Examinons maintenant graphiquement la qualité du modèle.
Au menu Fichier…Ouvrir, choisissons le fichier aaa.cor qui contient les résultats, puis cliquons sur Fichier…Voir, modifier les données :
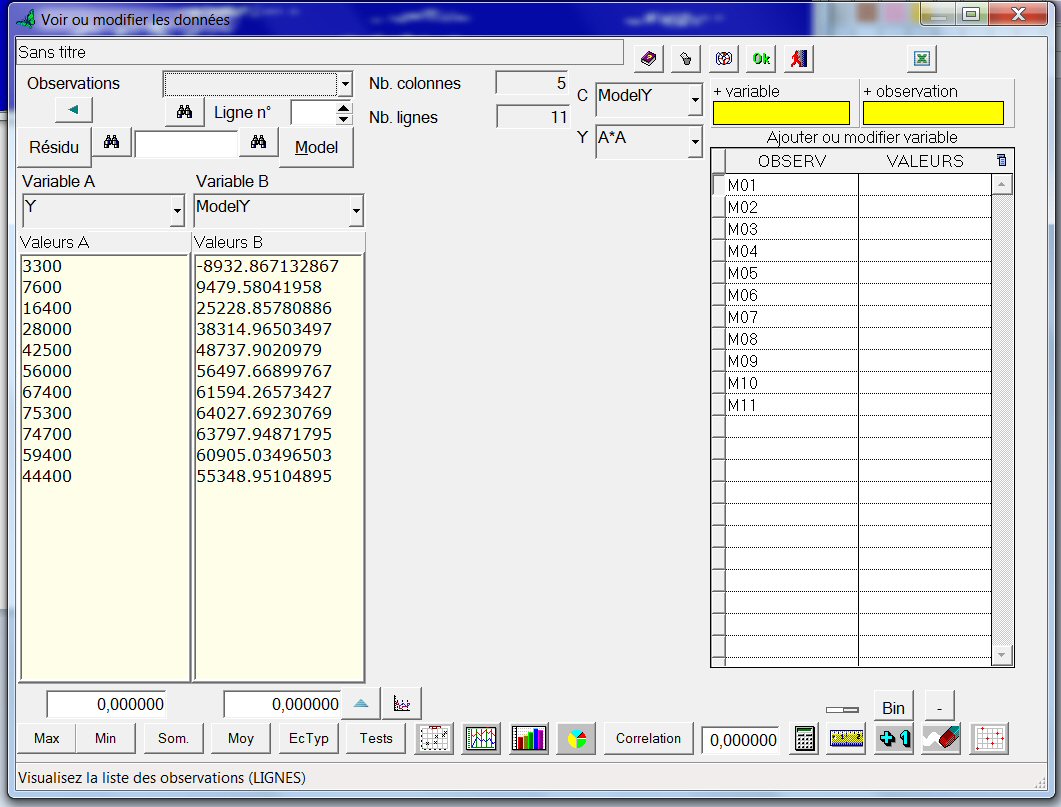

Les deux colonnes de gauche contiennent respectivement les valeurs mesurées Y et les valeurs restituées par le modèle. Cliquons sur le bouton ci contre , nous obtenons le graphe de ModelY en fonction de Y :
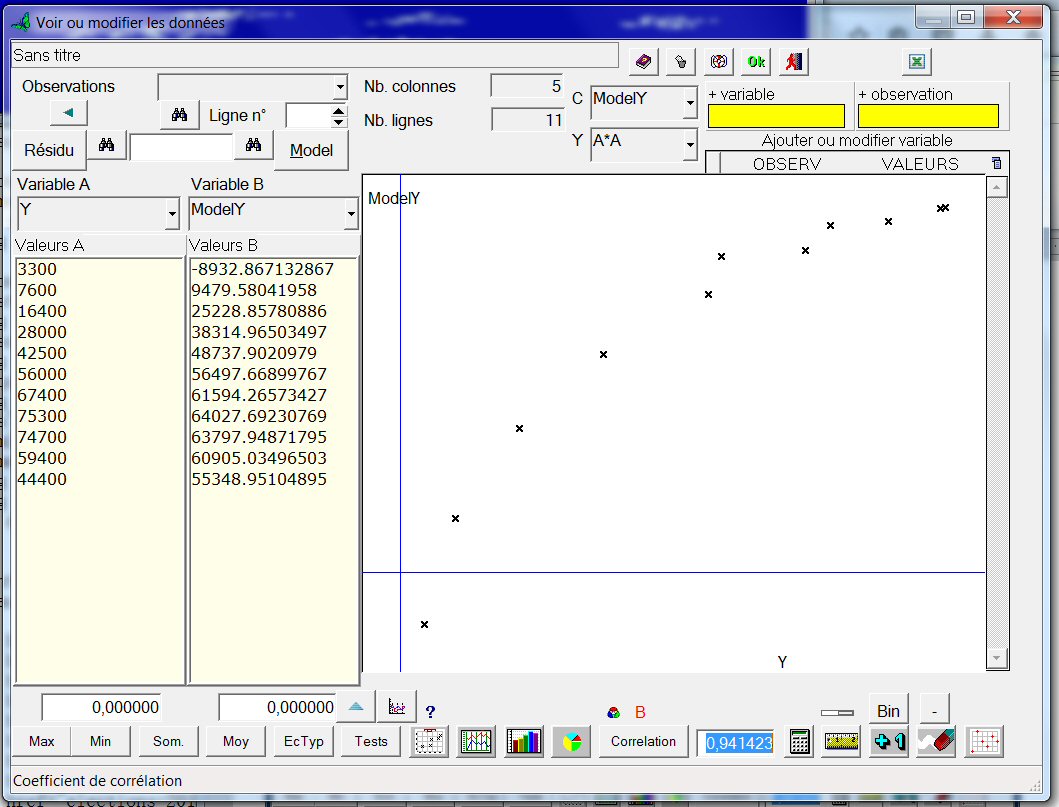

Si le modèle était correct, les points devaient être répartis sur la première bissectrice. Ce n’est pas le cas. Cliquons sur le bouton « Résidu ».
Puis cliquons sur le bouton ci-contre.
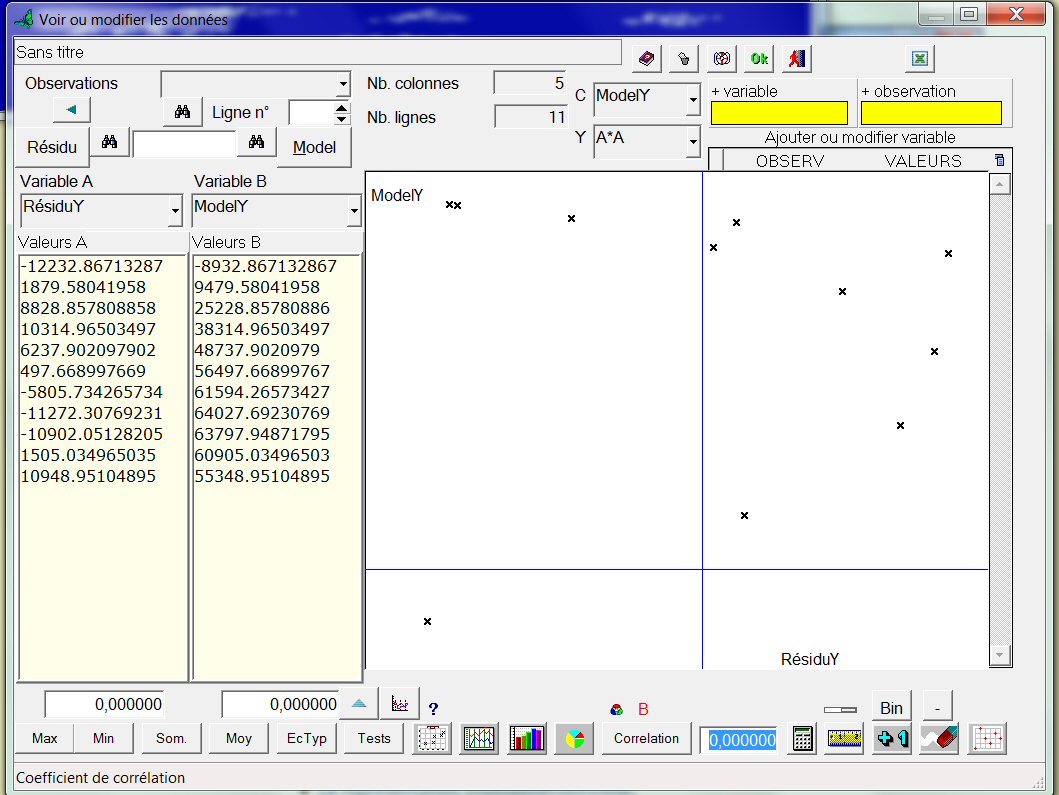
Il apparaît nettement que les résidus ne sont pas répartis de façon aléatoire, mais sous une forme plus ou moins parabolique. Le modèle polynomial d’ordre 2 est donc imparfait. On pourrait tenter un modèle polynomial d’ordre supérieur ; cependant, plus l’ordre du modèle augmente, plus le nombre de coefficients de l’équation est important (surtout s’il y a plus de 2 constituants dans le mélange) ; plus donc le nombre d’expériences nécessaires augmente, ce qui peut être rédhibitoire quand les expériences sont coûteuses.
C’est une autre solution que nous adoptons avec le logiciel CORICO :
Modèle avec interactions logiques
Revenons au menu Outils…Régression multiple, sélection à nouveau le fichier melangebinaire.cor qui contient le tableau de données. Par défaut le fichier résultat s’appellera aaa.cor :
Cette fois nous ne cochons pas « * seule », afin d’examiner toutes les interactions logiques, puis nous procédons exactement comme précédemment. Le modèle obtenu contient, par ordre d’importance décroissante, deux interactions logiques : A]-A et A}A, et un terme simple : A.

Les coefficients R2 ajusté et Q2 sont meilleurs que dans le modèle précédent.
Graphiquement, la qualité du modèle est meilleure ; les points se rapprochent de la bissectrice et les résidus sont aléatoires :
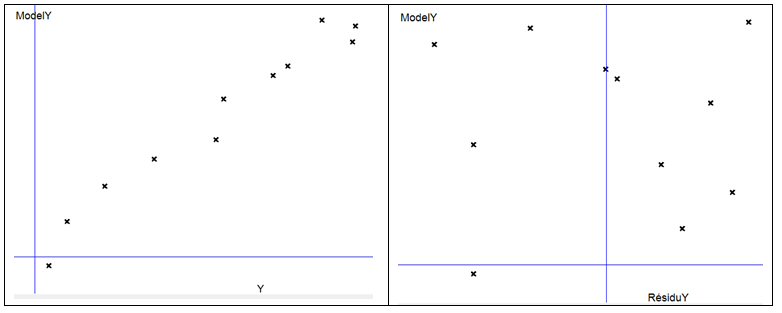

Dans les zones "Variable A" et "Variable B", sélectionnons respectivement Y et ModelY. Dans les zones "C" et "Y", sélectionnons respectivement A]A et A}A. Cliquons sur le bouton ci-contre et cochons "* coef." :
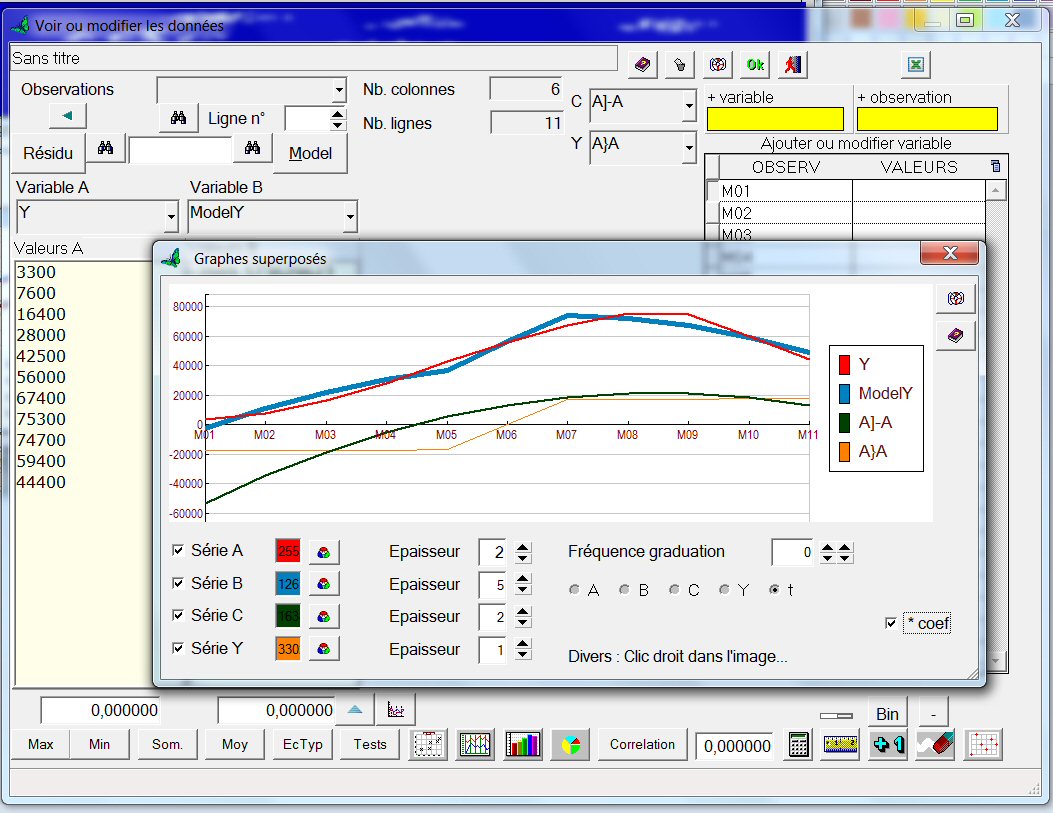
Ce graphe montre le modèle de Y comparé à Y, et l’allure des deux interactions logiques qui interviennent dans l’équation du modèle.
L’ajustement est relativement bon. Est-il possible de faire mieux ?
Modèle avec interactions logiques et fonctions sinusoïdales
Revenons au menu Outils…Régression multiple, sélectionnons à nouveau le fichier melangebinaire.cor qui contient le tableau de données. Par défaut le fichier résultat s’appellera aaa.cor. Mais cette fois, dans le cadre « Type de régresseurs », cochons aussi « Résonnances » afin de chercher si des termes sinusoïdaux ne pourraient pas être intégrés au modèle :
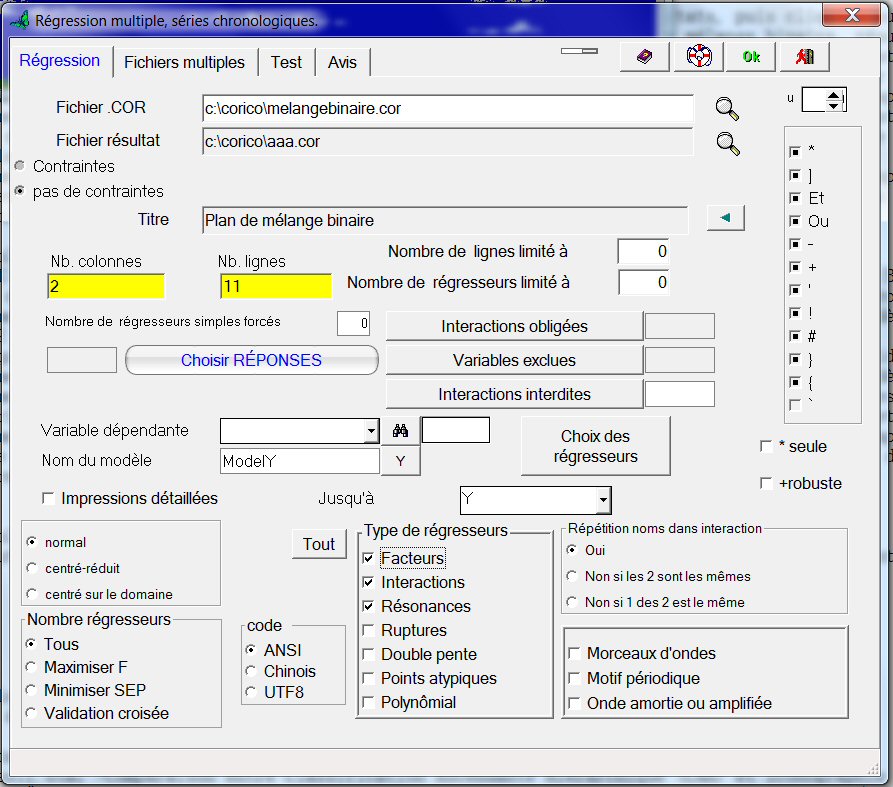
Puis nous procédons exactement comme précédemment. Le modèle obtenu ne contient finalement que des fonctions sinusoïdales :

Les coefficients R2a et Q2 sont excellents, et la représentation graphique le confirme : bon ajustement sur la bissectrice de ModelY en fonction de Y ; répartition aléatoire des résidus :
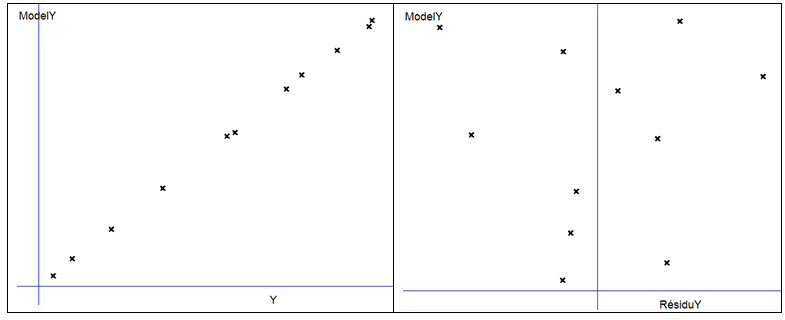
Les noms des variables sinusoïdales, dans une notation raccourcie propre à CORICO, seront mieux compris graphiquement :
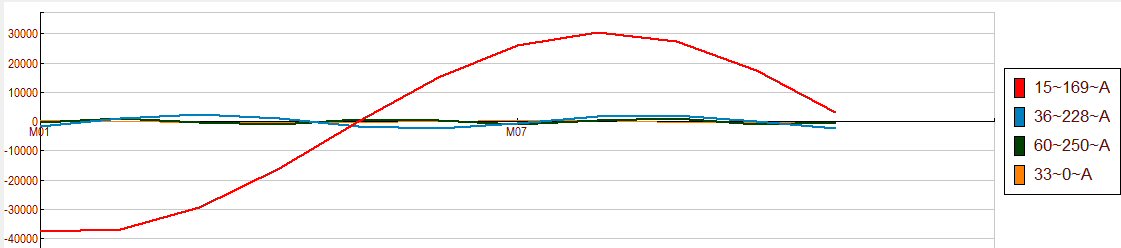
Si maintenant l’on compare la réponse à son modèle, ils se superposent presque exactement :
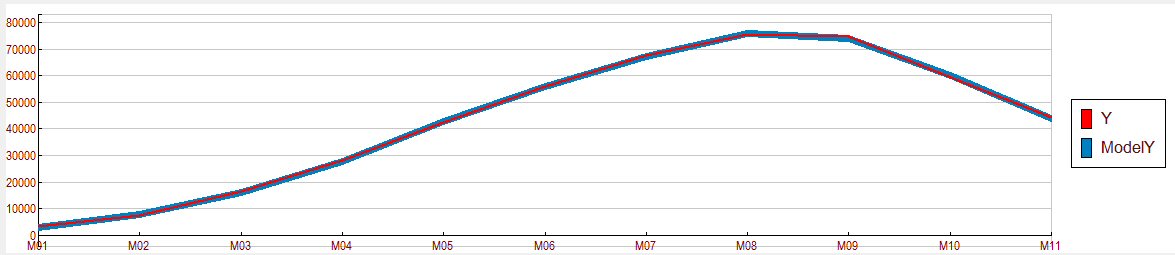
Validation du modèle
Muni des trois modèles, nous pouvons utiliser le solveur de CORICO, afin de
Il est toujours recommandé d’effectuer ensuite ces essais de validation. En effet, bien que les coefficients R2a et Q2 soient meilleurs pour le troisième modèle, il n’est pas garanti que le modèle soit effectivement plus prédictif. En effet, la décomposition d’un signal quelconque en une somme pondérée de fonctions sinusoïdales est toujours possible (du moins si le phénomène est « stationnaire »). Cependant, dans le présent cas, nous pouvons considérer le troisième modèle avec une certaine confiance, d’une part parce qu’il est parcimonieux (il contient peu de termes), d’autre part parce que le premier terme explique presque toute la variabilité de la réponse.
Optimisation de la réponse
A titre d’exemple du précédent paragraphe, voyons comment maximiser la réponse Y avec le solveur de CORICO appliqué au 3ème modèle.
Le solveur se trouve au menu Outils…OPTIMISATION multiréponses, PREVISION :
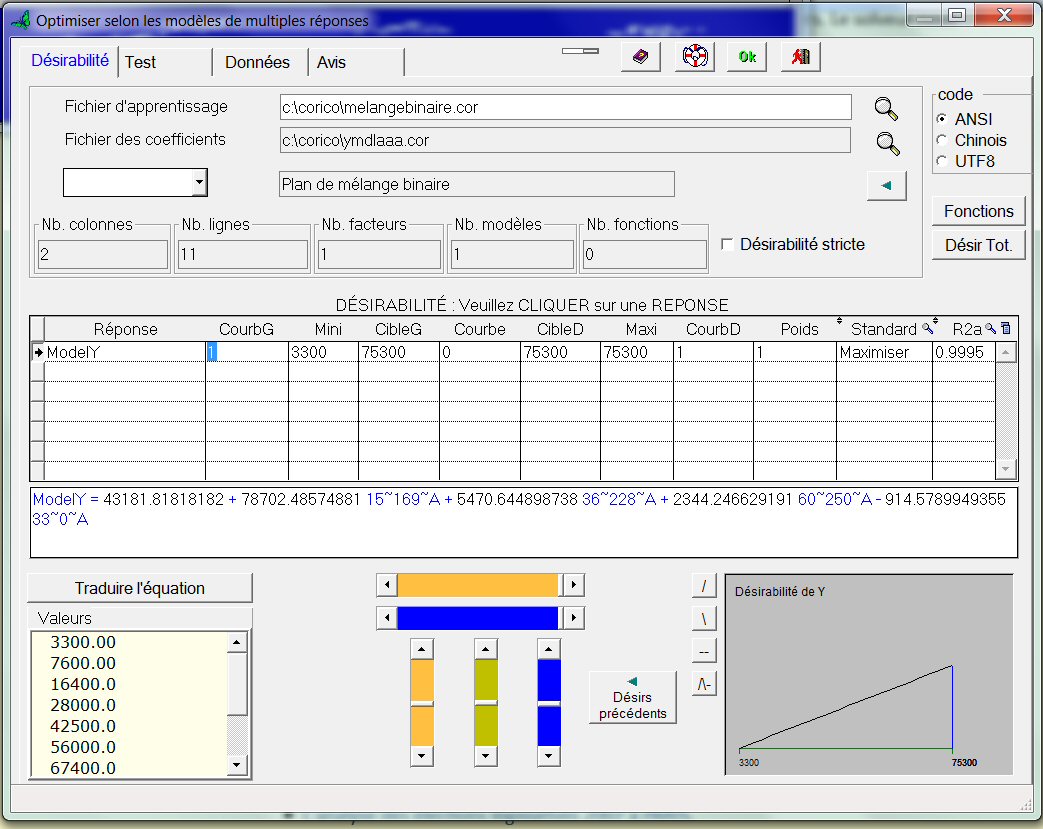
Lorsque vous cliquez sur la ligne de ModelY, vous voyez apparaître, en bas à droite, un graphe de désirabilité par défaut. Vous pourriez modifier ce graphe avec les ascenseurs, mais il nous convient ici, puisqu’il signifie que plus Y est grand (en abscisse) plus l’on est content (en ordonnée), car on souhaite maximiser Y. La valeur 75300 à droite du graphe est le maximum obtenu durant les expériences. Nous désirons faire mieux.
Cliquons sur l’onglet Test :
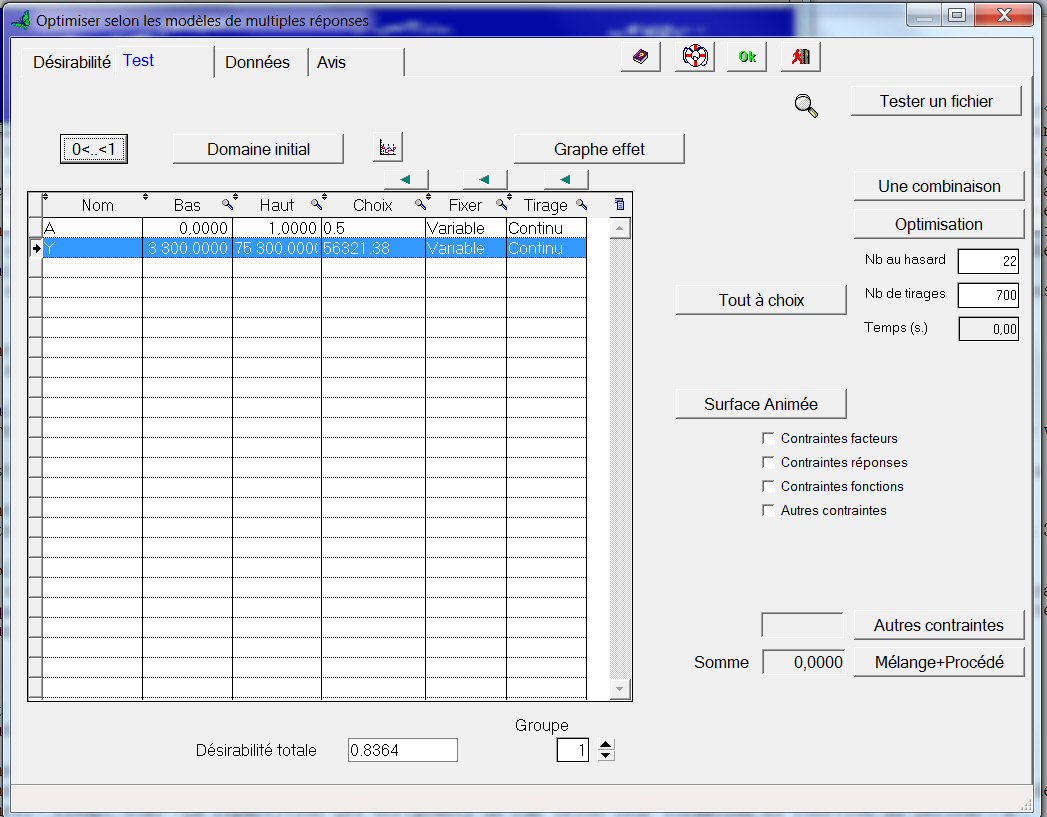
Dans les colonnes « Bas » et « Haut » du tableau, sont affichées par défaut les valeurs minimum et maximum obtenues pendant les expériences, pour A et pour Y.
Dans la colonne « Choix » est marquée par défaut la valeur moyenne de A, et la valeur du modèle de Y pour cette valeur de A.
Lorsque nous cliquons sur le bouton « Optimisation », des tirages aléatoires des valeurs de A sont effectués entre les valeurs Bas et Haut (méthode de Monte-Carlo). La valeur de A qui maximise la désirabilité est alors inscrite dans la colonne « Choix »:

La valeur optimale de Y est 76609,60, pour A = 0,7376809. Cette valeur du modèle de Y est supérieure au maximum obtenu pendant les expériences.
Il reste à effectuer une expérience de validation, afin de connaître le Y réel correspondant.
Voir aussi :
D'autres exemples de traitement de données avec CORICO :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.
Economisez des années en Recherche et Développement :
INDUSTRIE - RECHERCHE - QUALITÉ - ÉPIDÉMIOLOGIE - ENQUÊTES - ECONOMETRIE ...
FORMATION
- Découvrir et maîtriser
- l'Analyse de Donnéees
- le Plan d'expériences
- les Séries Temporelles
- Voir les formations