Analyse d’une réponse binaire avec CORICO
Lorsque la variable à expliquer n’a que deux modalités (par exemple, vrai/faux, oui/non, malade/pas malade, 1/0...), beaucoup de logiciels de statistiques proposent des méthodes différentes de celles utilisées pour les variables continues, et pas toujours d’emploi aisé (par exemple, régression logistique, arbre de décision…).
Dans le logiciel CORICO, l’introduction des « interactions logiques », permet de façon immédiate et facile, une même démarche pour les variables continues et pour les variables binaires.
Comparons, sur un exemple, trois approches disponibles dans CORICO : « Iconographie des corrélations », régression multiple et arbre de décision.
L’exemple de Quinlan (1993)
Il s’agit d’expliquer le comportement des individus par rapport à un jeu {jouer/ne pas jouer} à partir de données météorologiques :
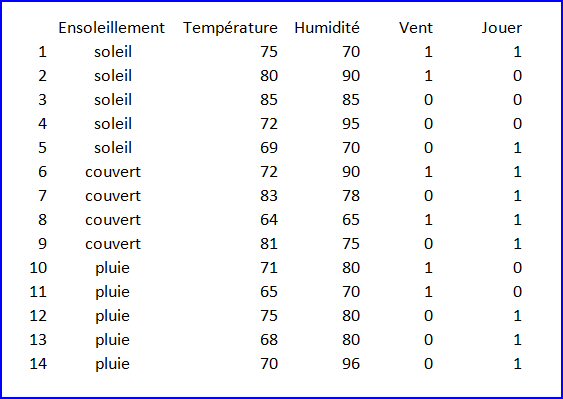
1. Iconographie des corrélations
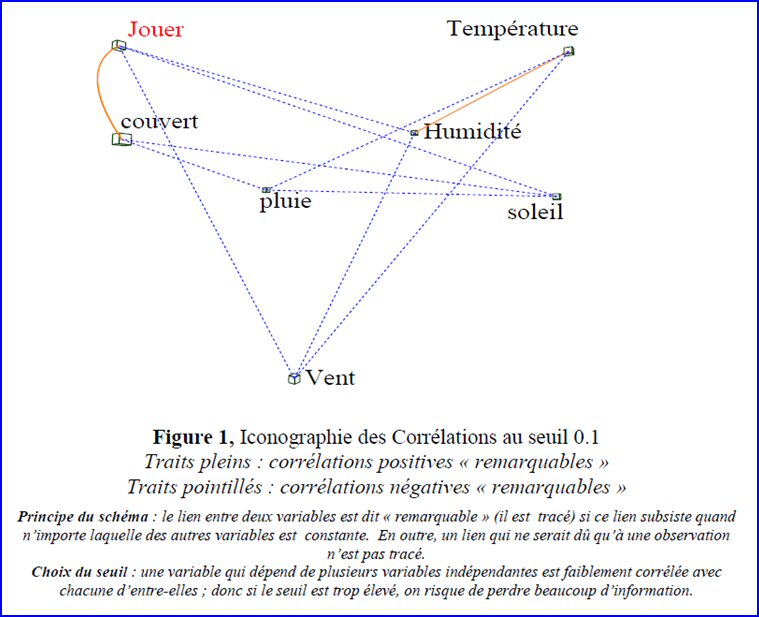
La figure montre que le soleil, le vent et l’humidité sont des facteurs négatifs pour le jeu considéré, et qu’on pratique plutôt ce jeu par temps couvert.
2. Modèle avec interactions logiques
En plus des variables simples, le logiciel CORICO puise ici dans un vivier de 210 « interactions logiques » (14 interactions possibles par couple de variables), et retient les plus pertinentes.
La régression multiple classique donne un bon ajustement grâce aux interactions logiques et permet d’éviter le recours à la régression logistique (d'ailleurs difficile ici vu le faible nombre d'observations) :

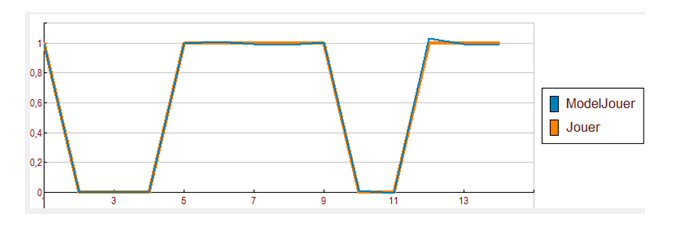
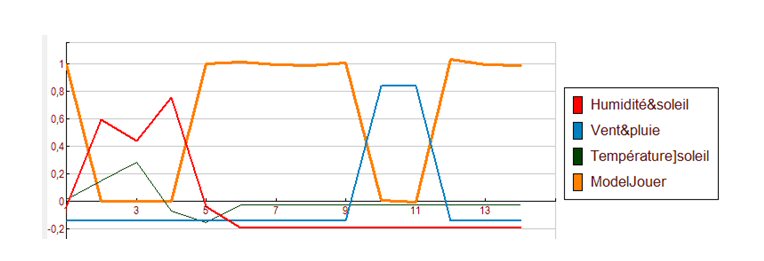
Chaque terme du modèle de CORICO explique le résidu non expliqué par les termes précédents :
On joue au jeu considéré (par ordre d’importance des trois premiers régresseurs) :
Le modèle ne contredit pas la vue d’ensemble donnée par l’Iconographie des corrélations. Le modèle a un rôle prédictif.
3. Segmentation et arbre de décision
Une autre façon d’aborder le problème est la segmentation :
Critère d’arrêt : la segmentation s’arrête dans une branche de l’arbre si
3.1 Segmentation sur les variables simples
Classiquement, la segmentation est pratiquée sur les variables simples. Commençons par là.
La figure suivante montre l’arbre entièrement déployé. Le groupe en surbrillance correspond à un temps non couvert, sans vent et sans soleil. Les éléments de ce groupe sont les numéros 12, 13, 14. Ils ont tous la valeur 1 pour « jouer » (colonne la plus à droite).
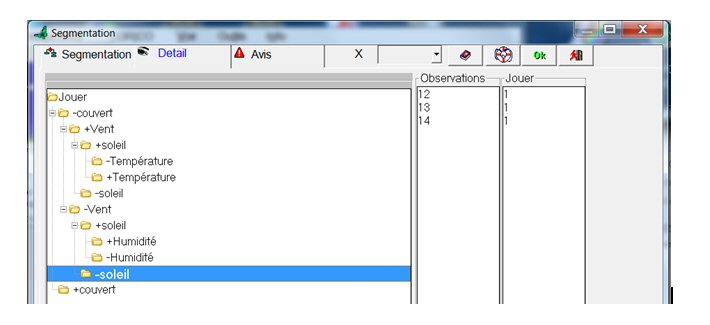
Mettons en surbrillance le groupe correspondant au temps couvert : ce sont les n° 6, 7, 8, 9 :
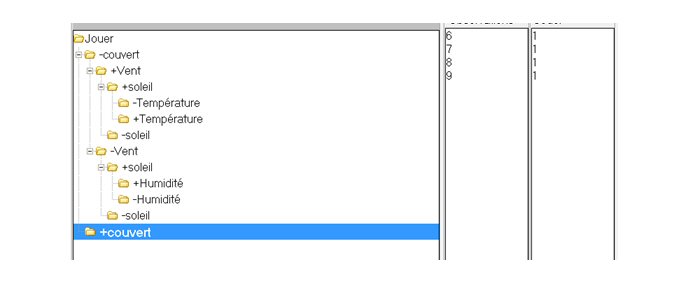
Un autre groupe correspond à un temps non couvert, sans vent, ensoleillé et non humide. Il ne comprend qu’un seul jeu (le n°5) :

Enfin, le dernier groupe qui contient un jeu (le n°1), correspond à un temps non couvert, venteux, ensoleillé et froid :
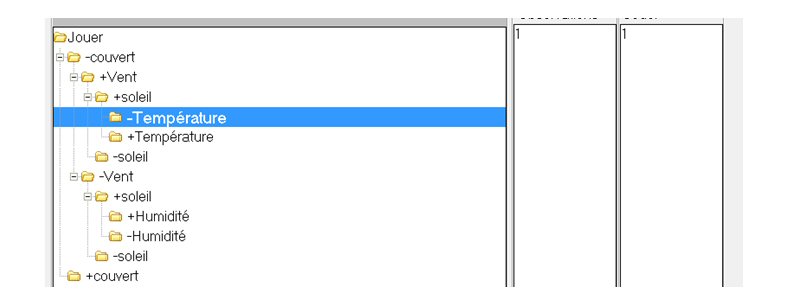
Tous les autres groupes contiennent des zéros (pas de jeu).
Ainsi, les périodes de jeu sont dispersées dans 4 groupes. Il est difficile d’en tirer une conclusion concise.
3.2 Les points faibles des arbres de décision
A chaque étape, le critère de partition dépend des classes déjà obtenues ; deux individus dans des classes différentes ne sont plus comparés.
Un autre reproche est l’incapacité, dans les algorithmes classiques (C4.5, CART, CHAID, etc.), à détecter les combinaisons de variables.
C’est ici que les interactions logiques nous permettent d’aller plus loin.
3.3 Segmentation sur variables simples et interactions logiques
Paradoxalement, l'ajout des interactions logiques aux variables simples simplifie l'arbre de décision !
l’arbre entièrement déployé contient moins de branches : un seul groupe suffit à expliquer tous les « jouer » = 1. En vertu des critères d’arrêt donnés plus haut, aucune des variables simples n’est apparue dans l’arbre de décision.
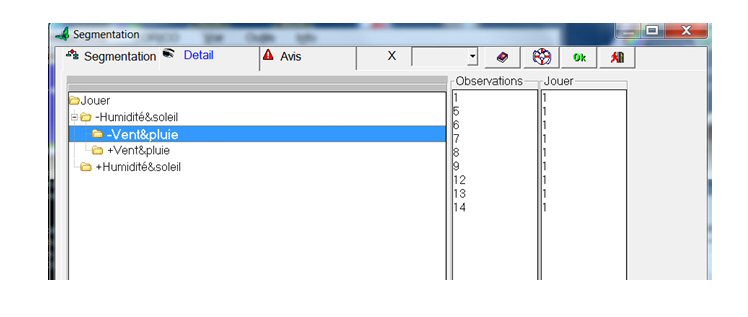
L’explication en terme météorologique concorde avec celle donnée au § 2 par la régression multiple : le groupe sans (humidité ET soleil) et sans (Vent ET pluie) contient les 9 observations avec jeu.
L’arborescence est essentiellement descriptive.
Conclusion de l'analyse d'une variable binaire
L’usage des interactions logiques améliore et simplifie l’analyse des variables binaires aussi bien que des variables continues. En effet, on puise dans un plus grand vivier de variables explicatives. Les trois approches concordent dans leurs conclusions.