Analyse des données du naufrage du Titanic
par la méthode CORICO

Le jeu de données "Kaggle" du Titanic, accessible ici, fait référence au naufrage du fameux paquebot le Titanic en 1912, où il y eut beaucoup de noyés à cause du nombre insuffisant de canots de sauvetage.

Il contient pour chaque passager les informations suivantes :

Après retrait des lignes avec valeurs manquantes, le tableau analysé contient 1045 personnes.

Difficulté

Ce mélange de variables qualitatives et quantitatives se prête mal à une analyse multivariée de type ACP.

Aussi allons-nous utiliser l'Iconographie des Corrélations, qui est un moyen intuitif, rapide et sûr d’appréhender l’essentiel d’un tableau de données. Il montre les liens remarquables entre les paramètres disponibles, en particulier les liens à la survie.

L’iconographie des corrélations

La figure 1 est tirée de la matrice de corrélation. Son principe est simple :

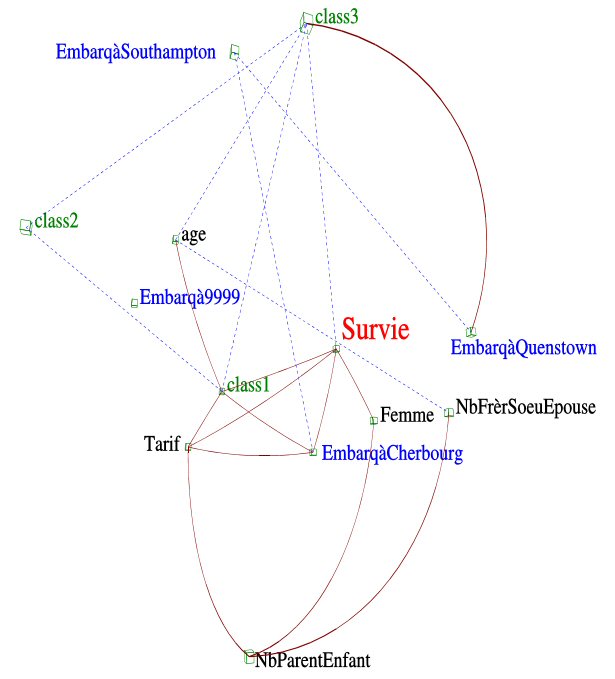
Informations apportées par la figure 1

Concentrons-nous d'abord sur les liens « remarquables » avec la survie :

L'interprétation est immédiate !

Voici les valeurs des coefficients de corrélations à Survie :

La figure 1 montre aussi que la classe 1 contient des gens plus âgés et payant plus cher. Ces gens ont plutôt embarqué à Cherbourg.

Lorsque le nombre de parents et enfants augmente, le nombre de frères, sœurs ou épouses augmente aussi, ainsi que la présence de femmes.

Modèles de survie

La figure 1 apporte de façon claire toute l'information. Mais pour prédire si tel ou tel passager à survécu, il est bon de construire un modèle de régresion.

Le second modèle de régression multiple est légèrement meilleur que le premier (R2 ajusté supérieur).

Dans les modèles de CORICO, les termes sont rangés par influence décroissante. Chaque terme expliquant le résidu non expliqué par les précédents. Les termes du second modèle sont des "interaction logique". Le logiciel arrête d’ajouter des termes quand l’erreur standard de prédiction (SEP) ne diminue plus.

Comparons la survie à son modèle

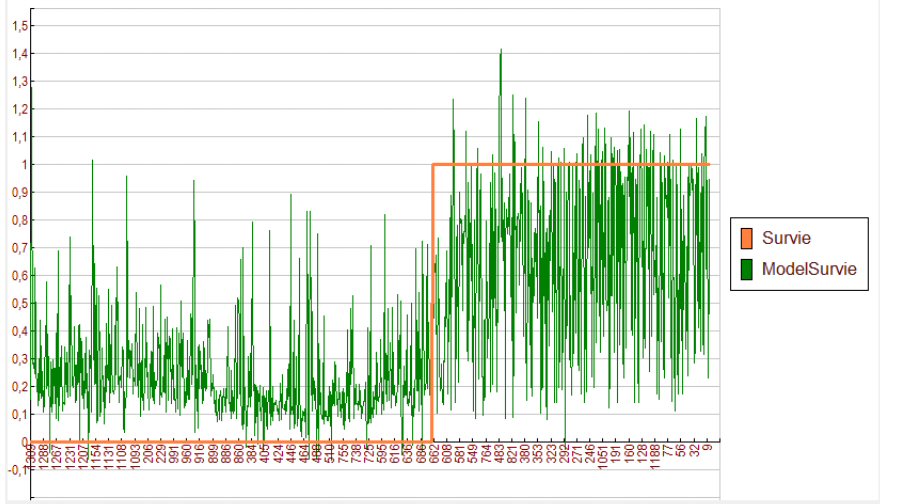
La survie, en orange, vaut 0 ou 1 ; en revanche le modèle, en vert, n’est pas binaire. La valeur 0.5 peut sembler un bon seuil de séparation entre survie ou non. Toutefois, CORICO nous offre un moyen de choisir le seuil optimal :

Cliquons sur le bouton « BIN », au menu Fichier…Voir, modifier les données : une fenêtre apparaît ; cliquons sur le bouton « Seuil optimum », alors une valeur apparaît dans la zone « Seuil choisi » : 0.3480083674326. C’est celui qui capture le plus de vrais positifs, avec le moins de faux positifs.

Toutes les fois que le modèle est supérieur à 0.348, les chances de survie s’élèvent à 78% comme il est indiqué dans la fenêtre ci-dessous.

Cliquons sur le bouton « Courbe ROC » :

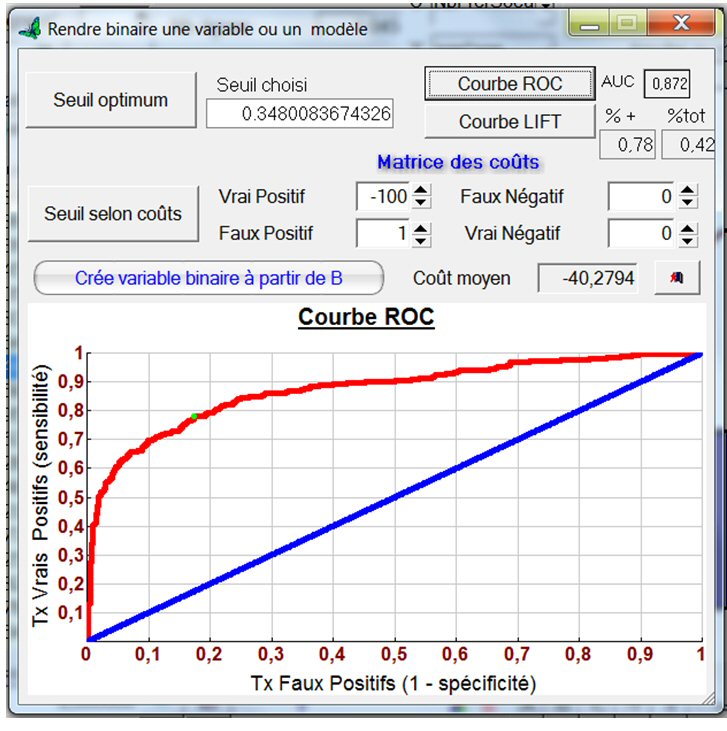
La courbe ROC donne, lorsqu’on fait varier le seuil, le rapport du taux de vrais positifs (les Survies prévues qui sont réellement des survies) sur le taux de faux positifs (les survivants prévus qui n’ont pas survécu). Ces deux taux augmentent avec la valeur du seuil.

Le point vert dans la courbe rouge, correspond au seuil optimum (qui donne 78% de vrais positifs) : c’est le point le plus proche du coin en haut à gauche du graphe.

La droite bleue est la courbe ROC que l’on obtiendrait si le modèle prédisait au hasard positif ou négatif : il y aurait alors autant de vrais que de faux positifs quel que soit le seuil.

A droite du bouton « Courbe ROC » on lit AUC = 0.872.
AUC (« Area under curve ») est la surface sous la courbe rouge. Plus AUC est proche de 1 plus le nombre de vrais positifs est grand par rapport au nombre de faux positifs, quel que soit le seuil. Aussi AUC est un bon critère de comparaison entre plusieurs modèles.

Conclusion : tirer l'essentiel du tableau

Dans le logiciel CORICO, vous n'avez rien à programmer.

L’iconographie des corrélations, simple dans son principe, accessible à tous, permet de ne rien laisser passer d’essentiel dans un tableau de données, tout en éliminant les redondances et les "fausses bonnes corrélations" c'est à dire les liens qui ne sont pas directs, mais causés par une tierce variable.

L'un des avantages des modèles avec interactions logiques, c'est qu'ils sont parfaitement explicables. Les "interactions logiques" sont des couplages de paramètres extrêment fréquent en pratique, et faciles à expliquer.

Voir aussi :

Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.