Un plan de mélange ternaire avec CORICO
Dans ce didacticiel, nous verrons, sur un exemple simple, la démarche de génération et d’analyse d’un plan d’expériences de mélange avec le logiciel CORICO. Plusieurs modèles seront comparés.
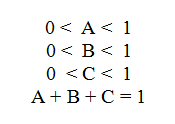
Un mélange ternaire à 3 constituants A, B et C doit respecter les contraintes ci-contre.
Prenons l’exemple d’un plan d’expériences décrit par PhanTan Luu. On cherche à mesurer l'efficacité d'un diluant formé de trois constituants : lactose, CaCO3 et cellulose.
La réponse choisie pour évaluer cette efficacité consistera à mesurer la dureté d'un matériau.
Comment générer un plan de mélange ternaire avec CORICO ?
Choisissez un nom de fichier, par exemple melangeternaire.cor ; Sélectionnez « Simplexe centré de Scheffé », « Nombre de facteurs » = 3, puis saisissez les noms des constituants : Lactose, CaCO3 et Cellulose :
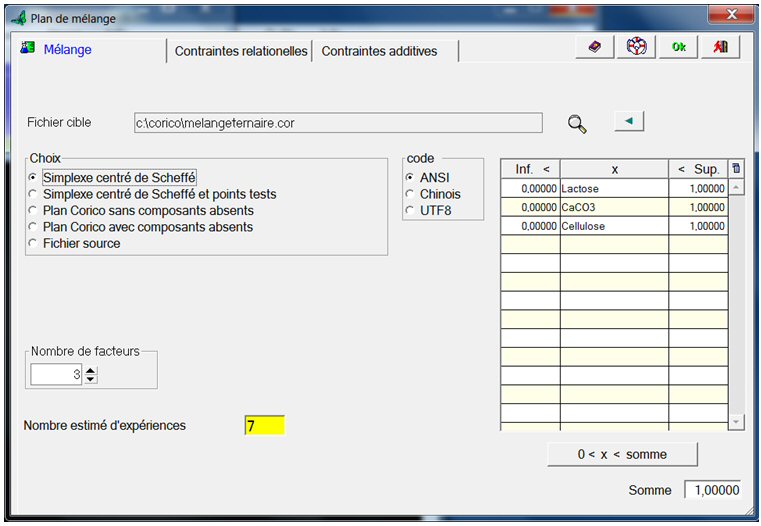
Le simplexe centré de Scheffé comprend 6 expériences, plus un point au centre, soit 7 expériences. Cliquons OK. Le plan est créé.

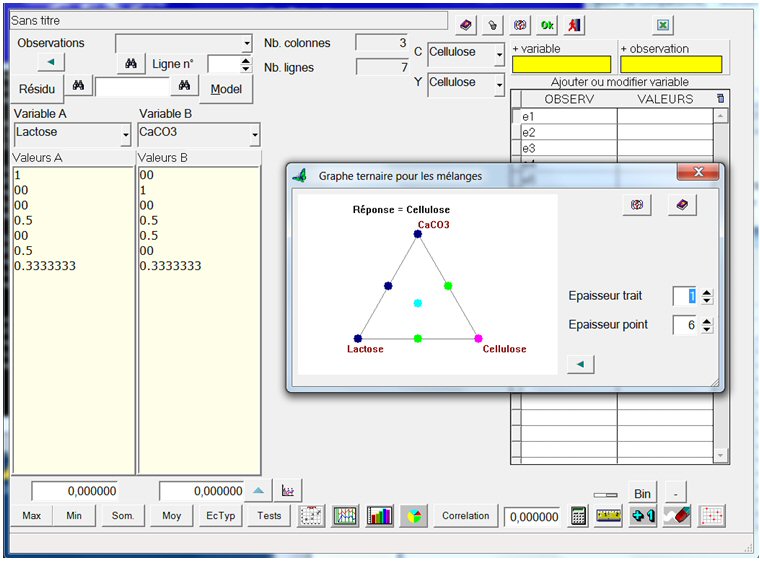
Un graphe ternaire apparaît, avec les trois constituants dans les coins correspondants au mélange pur. Un point, au milieu du côté Lactose – Cellulose, par exemple, correspond au mélange comprenant 50% de lactose, 50% de cellulose, et 0% de CaCO3. Le point au centre correspond au mélange en proportions égales de chacun des constituants.
La couleur des points correspond, en principe, à la réponse, des valeurs fortes (rouge) aux valeurs faibles (bleu foncé). Mais comme les expériences n’ont pas encore été réalisées, le logiciel a pris, comme « réponse » par défaut, le dernier des constituants, à savoir Cellulose.

Cliquez sur le bouton ci-contre pour voir l’ensemble du plan :
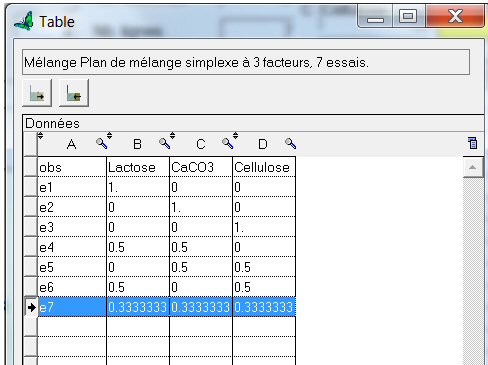
Le plan que nous venons de générer est le « simplexe centré de Scheffé ». En réalité, nous allons analyser un plan déjà existant, qui ne comportait pas le point au centre e7, mais une répétition des 6 autres points, soit 12 expériences.
Conseil : lorsque les expériences sont coûteuses, il est préférable de réaliser seulement 7 expériences, dont le point au centre, ou, mieux, 10 expériences (plan « simplexe centré de Scheffé et points tests », appelé aussi « plan de mélange centré augmenté ») plutôt que 12 expériences (6 expériences répétées 2 fois).
Analyse du plan avec CORICO
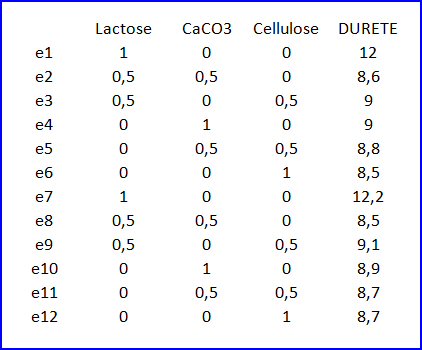
Une fois, les expériences réalisées, le tableau de données (6 expériences répétées 2 fois) comprend une colonne de plus : la dureté.
Ce plan présente l’inconvénient de ne jamais comprendre plus de deux constituants du mélange à la fois ; mais il nous permettra de mieux souligner les problèmes de modélisation.
Au menu Outils…Régression multiple, sélectionnons le fichier melangeternaire.cor qui contient le tableau de données. Par défaut le fichier résultat s’appellera aaa.cor :
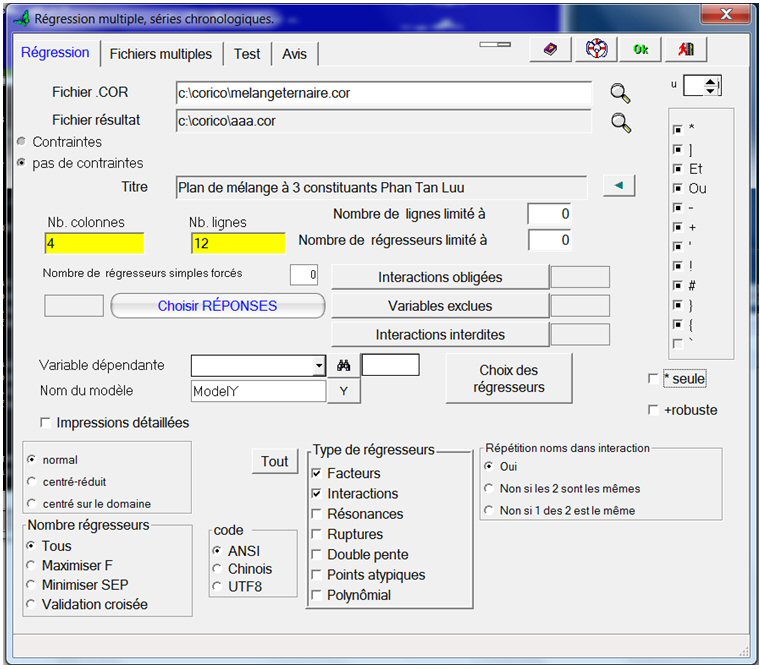
Cliquez sur le bouton « Choisir réponses », puis sur la variable « Dureté », elle passe à droite dans la colonne des réponses :
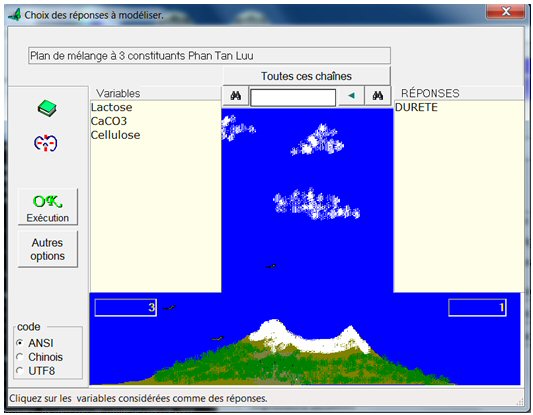
Cliquez sur « OK Exécution ». Alors le modèle est calculé :
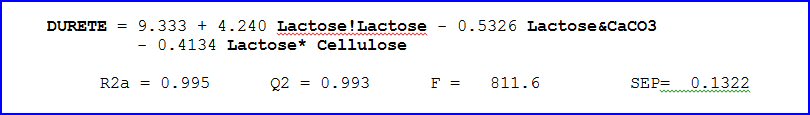
Ce modèle comprend des interactions logiques rangées par importances décroissantes : chaque terme de l’équation expliquant le résidu non expliqué par les précédents. L’ajout de terme s’arrête quand l’erreur standard de prédiction (SEP) ne diminue plus.
Les coefficients R2ajusté et Q2, permettent respectivement d’évaluer les qualités descriptives et prédictives du modèle. Ils doivent être le plus proches de 1 possible. Le F de Fischer-Snedecor (rapport de la fraction expliquée par le modèle sur la fraction résiduelle) doit être le plus fort possible. SEP, erreur standard de prédiction doit être la plus faible possible.
Examinons maintenant graphiquement la qualité du modèle.
Au menu Fichier… Ouvrir, choisissons le fichier aaa.cor qui contient les résultats, puis cliquons sur Fichier…Voir, modifier les données.
Les deux colonnes de gauche contiennent respectivement les valeurs mesurées Y et les valeurs restituées par le modèle.

Cliquons sur le bouton ci-contre, nous obtenons le graphe de ModelDureté en fonction de la Dureté :
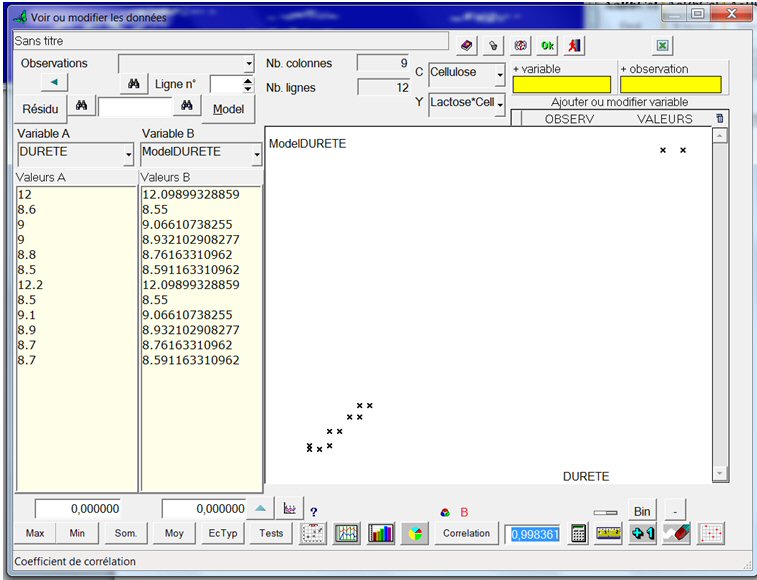

Les points sont assez bien répartis sur la première bissectrice. Cliquons sur le bouton « Résidu » puis de nouveau sur le bouton ci-contre :
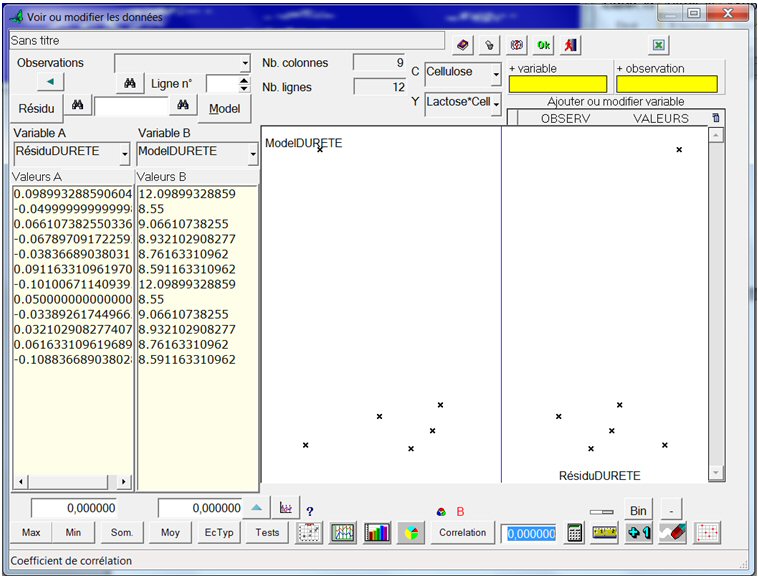
Les résidus (en abscisse) sont répartis aléatoirement. Nous pouvons donc accorder une assez bonne confiance au modèle.
Optimisation
Muni de ce modèle, nous pouvons utiliser le solveur de CORICO, afin de
Supposons que l’on souhaite minimiser la dureté.
Le solveur se trouve au menu Outils…OPTIMISATION multiréponses, PREVISION :
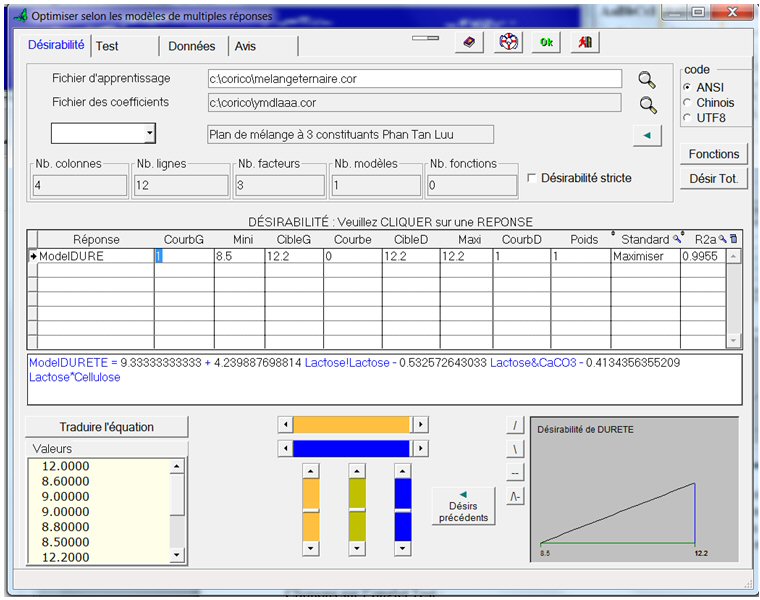
Lorsque vous cliquez sur la ligne de ModelDureté, apparaissent, en bas à droite, un graphe de désirabilité par défaut, et, en dessous du tableau, l’équation du modèle. Si vous cliquez sur le bouton « Traduire l’équation », les interactions logiques contenues dans l’équation sont traduites en français clair :

Nous allons modifier le graphe de désirabilité par défaut. Actuellement, il signifie que plus la Dureté grande (en abscisse) plus l’on est content (en ordonnée). Or nous souhaitons au contraire minimiser la Dureté. La valeur 8.5 à gauche du graphe est le minimum obtenu durant les expériences. Nous désirons faire mieux.

Cliquons sur le bouton « \ » ; vous obtenez le graphe de désirabilité cicontre.
Il signifie que plus la Dureté est faible (en abscisse) plus l’on est content (en ordonnée).
Cliquons sur l’onglet Test :
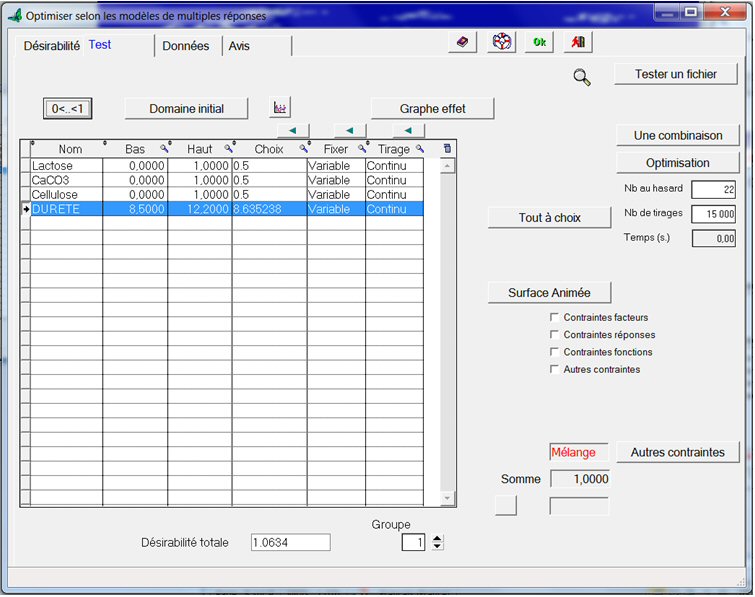
Dans les colonnes « Bas » et « Haut » du tableau, sont affichées par défaut les valeurs minimum et maximum obtenues pendant les expériences, pour les constituants et pour la réponse Dureté. Le logiciel a détecté qu’il s’agit d’un mélange (mention « mélange » en rouge), car la somme des constituants est constante durant les essais.
Dans la colonne « Choix » sont marquées par défaut les valeurs moyennes des constituants.
Lorsque nous cliquons sur le bouton « Optimisation », des tirages aléatoires des valeurs des constituants sont effectués entre les valeurs Bas et Haut (méthode de Monte-Carlo) ; et celles qui maximisent la désirabilité sont alors inscrite dans la colonne « Choix », ainsi que la Dureté calculée par le modèle pour ces choix. :
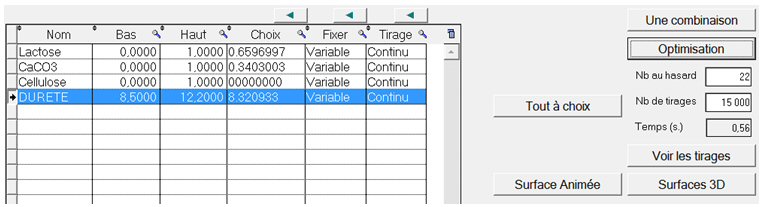 Selon ce modèle, la valeur optimale de Dureté serait 8.32, pour les proportions suivantes des constituants :
Selon ce modèle, la valeur optimale de Dureté serait 8.32, pour les proportions suivantes des constituants :
Lactose = 0,65969977
CaCO3 = 0,3403003
Cellulose = 0.
Il resterait à faire un essai réel de validation de ces valeurs de la colonne choix.
Mais comme il a été dit au début, le plan choisi présente l’inconvénient de ne jamais comprendre plus de deux constituants du mélange à la fois. Ce qui n'est pas recommandé.
Aussi, allons faire quelques vérifications.
Graphe ternaire
Cliquons sur le bouton « Voir les tirages, et sélectionnons respectivement Lactose dans « Variable A » , CaCO3 dans « Variable B », Cellulose dans « C » et ModelDureté dans « Y ».

Enfin, cliquons sur le bouton ci contre pour obtenir le graphe ternaire :
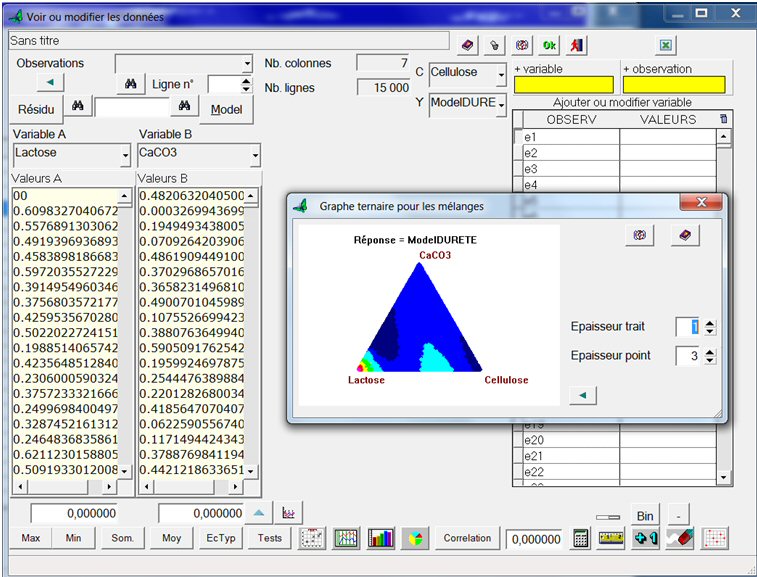 Dans un graphe ternaire, les sommets du triangle correspondent au mélange pur (un seul composant).
Dans un graphe ternaire, les sommets du triangle correspondent au mélange pur (un seul composant).
Le maximum de dureté se trouve dans la zone rouge (lactose pur) ; mais nous souhaitons minimiser la dureté : la zone optimale, selon ce modèle, correspond donc au centre de la grande zone bleu foncé, et sur le bord Lactose – CaCO3 du triangle.
Six modèles comparés
Avant de faire un essai de validation, qui, forcément, a un coût, il ne coûte rien d’essayer d’autres modèles.
Retournons Au menu Outils…Régression multiple, sélectionnons le fichier melangeternaire.cor qui contient le tableau de données. Par défaut, le fichier résultat s’appelle aaa.cor :
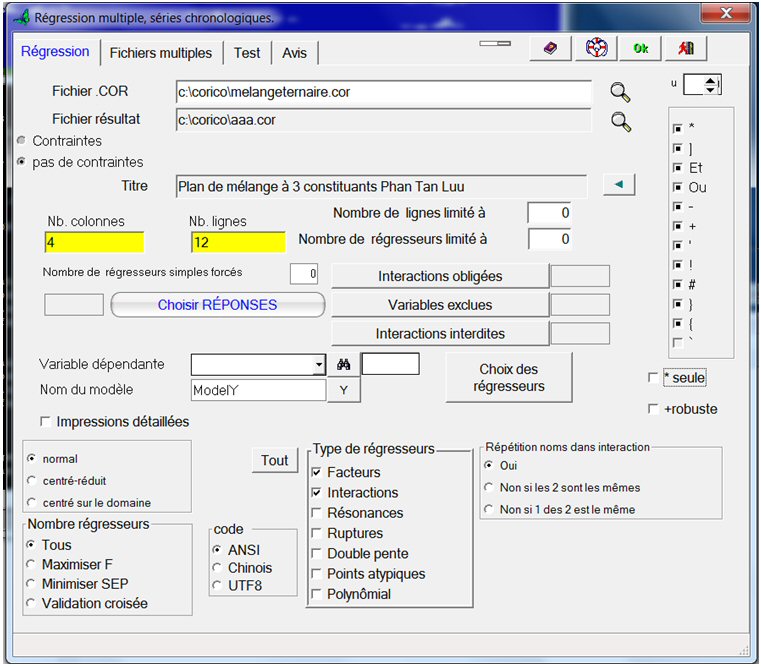 Pour le modèle précédent, nous n’avions coché
Pour le modèle précédent, nous n’avions coché
Essayons diverses combinaisons de ces options, en procédant ensuite exactement comme précédemment. Puis comparons les résultats pour chacun des modèles :
 Les modèles (2) et (4) sont identiques. Ce sont des modèles polynomiaux classiques.
Les modèles (2) et (4) sont identiques. Ce sont des modèles polynomiaux classiques.
Les trois premiers prédicteurs des modèles (1) et (3) sont identiques. Tous ces modèles ont d’excellent R2 ajusté et Q2, même si le premier modèle est légèrement meilleur de ce point de vue. Le troisième modèle a un moins bon F, car il est moins parcimonieux (il a plus de prédicteurs). Par contre, son erreur standard de prédiction (SEP) est nulle ! Le modèle (5) donne un graphe proche de celui du modèle (2)
Ce qui frappe, malgré des R2 ajustés presque identiques, c’est la différence des graphes ternaires et, donc, les valeurs fort différentes des essais de validation proposés :
Note : la différence entre les graphes ternaires aurait certainement été peu accusée si, au lieu de 6 essais répétés deux fois, nous avions réalisé d'emblée (comme il est recommandé) les 10 essais du plan simplexe centré de Scheffé augmenté, qui permet de mieux couvrir le domaine expérimental.
 Pour trancher entre les différents modèles, il est indispensable de rajouter au moins un point au centre, et, si possible dans un deuxième temps, les points tests du « plan simplexe centré de Scheffé et points tests » proposé par CORICO.
Pour trancher entre les différents modèles, il est indispensable de rajouter au moins un point au centre, et, si possible dans un deuxième temps, les points tests du « plan simplexe centré de Scheffé et points tests » proposé par CORICO.
En bleu, les essais déjà réalisés ; en rouge, les points de validation recommandés. Les points rouges, situés à l’intérieur du domaine expérimental, présentent l’avantage de comprendre chacun un mélange de l’ensemble des composants.
Une fois la (ou les) expérience(s) faite(s), et ajoutée(s) au tableau de données, nous pourrons affiner les modèles.
Conclusion
Dans cet exemple, l’analyse a pu sembler un peu longue car nous avons pris exprès un plan d'expériences sans points à l’intérieur du domaine expérimental.
Dans la pratique, si vous utilisez d’emblée le plan recommandé, l’analyse sera rapide : le premier modèle suffira dans la plupart des cas.
Voir aussi :
D'autres exemples de traitement de données avec CORICO :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.
Economisez des années en Recherche et Développement :
INDUSTRIE - RECHERCHE - QUALITÉ - ÉPIDÉMIOLOGIE - ENQUÊTES - ECONOMETRIE ...
FORMATION
- Découvrir et maîtriser
- l'Analyse de Donnéees
- le Plan d'expériences
- les Séries Temporelles
- Voir les formations