Classer des cancers en bénin ou malin
Avec le logiciel CORICO

Exemple

Le jeu de données proposé par le docteur William H. Wolberg (University of Wisconsin Hospitals, Madison) contient 699 observations. Chaque observation correspond à des caractéristiques de cellules issues d’une biopsie mammaire mesurées sur des patientes souffrant de cancer du sein classé bénin ou malin.

La variable à expliquer est «MALIGNE » qui vaut 4 pour un cancer malin et 2 pour un cancer bénin. Les variables explicatives sont :

Si l’on retire les lignes avec valeurs manquantes, il reste 683 lignes.

L’iconographie des corrélations montre les relations entre les facteurs liés aux cancers malins :

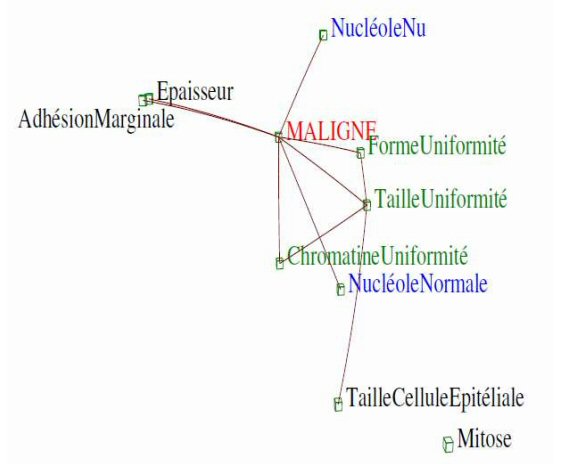
Iconographie des corrélations au seuil 0.3

Les liens représentent les corrélations « remarquables », c’est-à-dire ceux qui subsistent même si n’importe quelle des autres variables disponibles demeure constante.

Modèle d’apprentissage sur les 200 premières valeurs

Nous utilisons les 200 premières observations en tant qu’échantillon d’apprentissage et les 683 observations en tant qu’échantillon à prédire.

Voici le modèle de régression multiple CORICO tiré des 200 premières observations :

Ce modèle CORICO contient 3 termes qui sont des « interactions logiques ».

Dans CORICO, les termes du modèle sont classés par importance décroissante. Chaque terme explique le résidu non expliqué par les termes précédents.

Ici le premier terme est « TailleUnifor^FormeUniformité », qui signifie « TailleUniformité OU FormeUniformité ». Son coefficient est plus de trois fois plus important que celui du second terme, et six fois plus important que celui du troisième terme.

Prédiction :

Si on utilise ce modèle pour prédire l’ensemble des données, voici le résultat. Le graphe compare le réel qui est binaire (0 ou 1) à la prévision par le modèle :

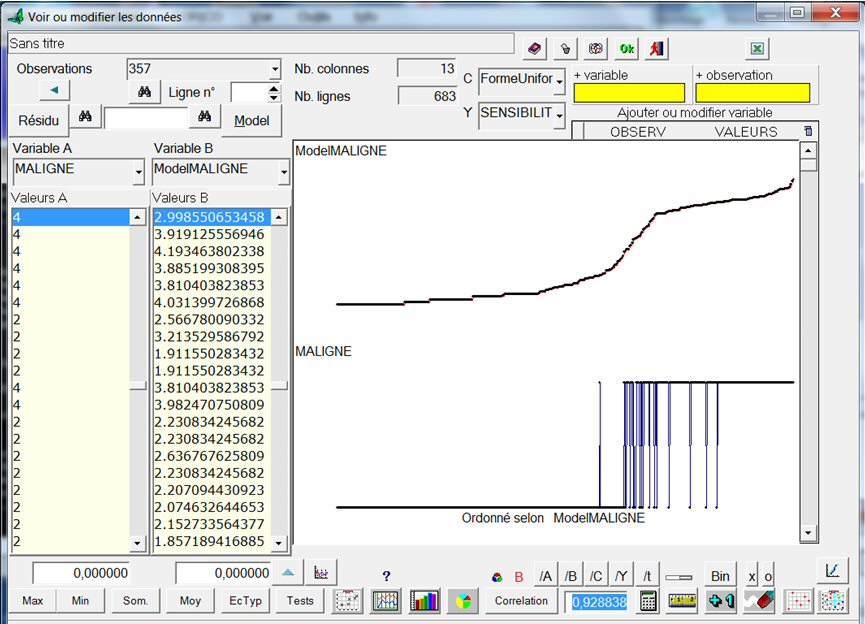
Ce modèle continu présente l’avantage d’une plus grande précision, et donc d’une plus grande sûreté qu’un modèle binaire : plus la valeur est forte plus la prédiction a des chances d’être juste.

Modèle binaire

Cependant, si nous préférons construire une variable prédictive binaire, valant 0 pour un score < seuil de modèleMALIGNE, et valant 1 sinon, il faut choisir un seuil. Voyons comment faire avec CORICO.

Pour choisir le seuil, cliquons sur le bouton BIN, puis sur « Seuil Optimum » :

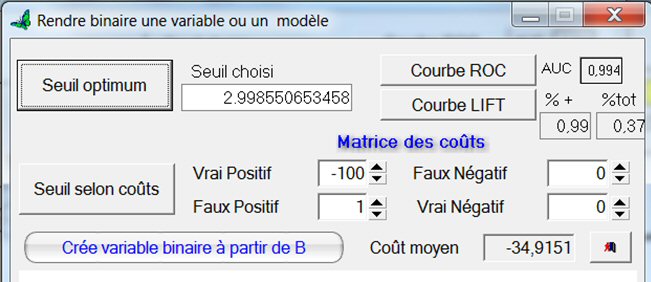
Le seuil optimum trouvé = 0,2998550653458. C’est celui qui capture le plus de vrais positifs, avec le moins de faux positifs.

Les chiffres « 0.99 » et « 0.37 », sur la droite, indiquent qu’à ce seuil, qui retient seulement les 37% meilleurs scores parmi l’ensemble des individus du fichier, on balaye déjà 99% des vrais positifs.

Sur la courbe, le seuil est maintenant signalé par le point rose :

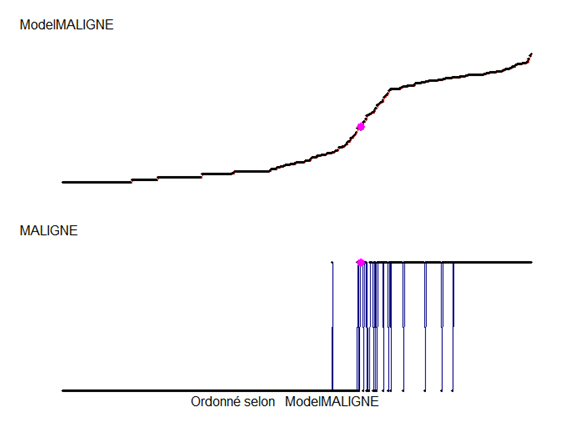
Cliquons sur le bouton « Courbe ROC » :

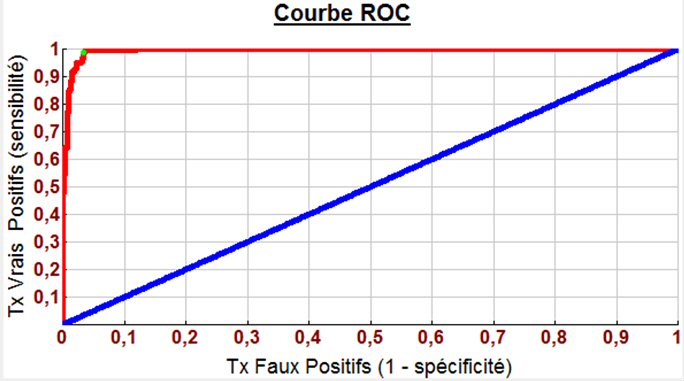
Le point vert dans la courbe rouge, correspond au seuil optimum (qui donne 99% de vrais positifs) : c’est le point le plus proche du coin en haut à gauche du graphe.

La droite bleue est la courbe ROC que l’on obtiendrait si le modèle prédisait au hasard positif ou négatif : il y aurait alors autant de vrais que de faux positifs quel que soit le seuil.

A droite du bouton « Courbe ROC » on lit AUC = 0.994.

AUC (« Area under curve ») est la surface sous la courbe rouge. Plus AUC est proche de 1 plus le nombre de vrais positifs est grand par rapport au nombre de faux positifs, quel que soit le seuil. Aussi AUC est un bon critère de comparaison entre plusieurs modèles.

Maintenant, cliquons sur le bouton « Créer variable binaire à partir de B » après avoir choisi un nom de variable dans le champ « +variable » :

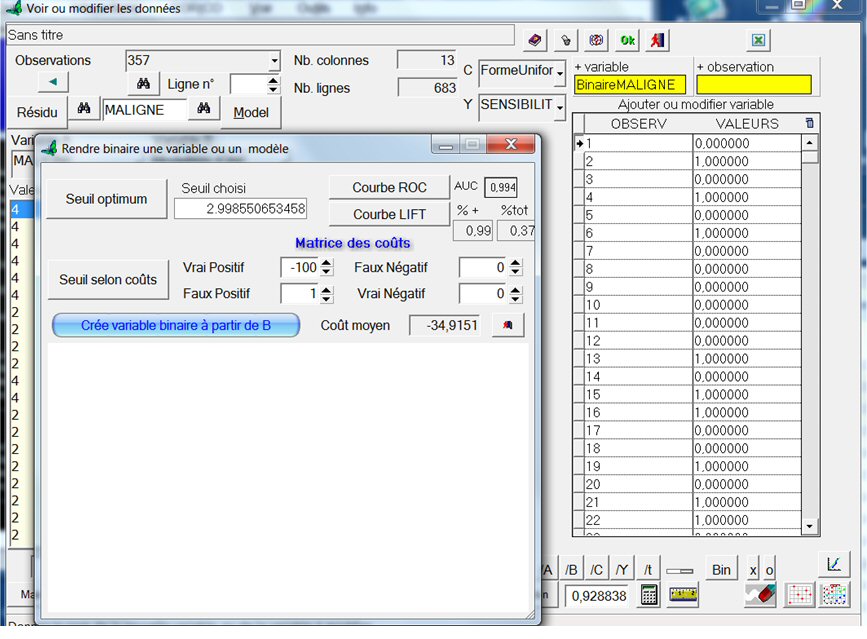
Notre variable binaire est créé. Cliquons sur le bouton OK pour l’enregistrer, puis sur le bouton pour afficher son graphe :

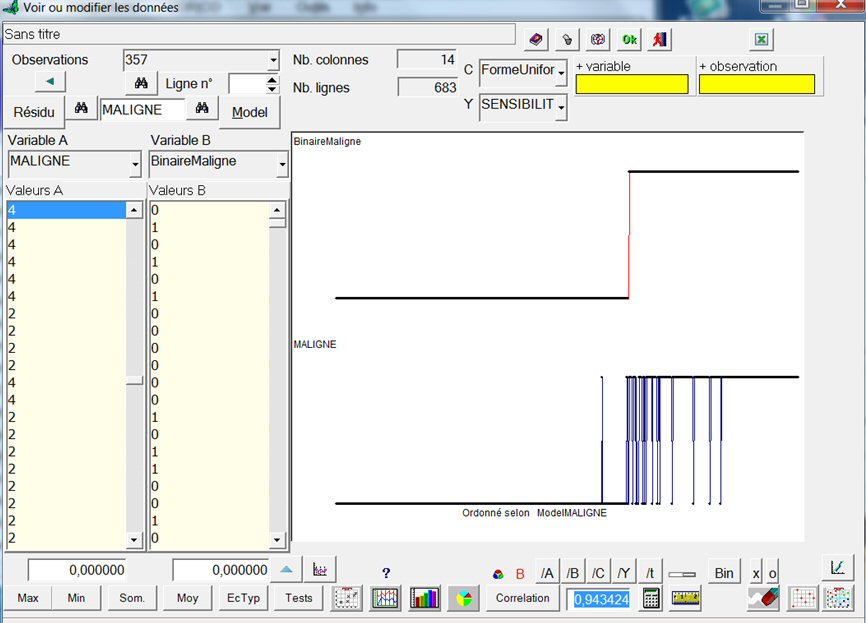
Cette variable binaire prédit les cancers malins avec 99% de vrais positifs.

Voir aussi :

---

Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.