Une alternative aux corrélations canoniques.
Conditions des règles de conduite.
L’analyse des « corrélations canoniques » proposée en 1936 par Hotelling, cherche à décrire les relations linéaires qui existent entre deux ensembles de variables mesurées sur les mêmes individus.
On utilise des combinaisons linéaires des variables de chaque groupe. Ces combinaisons sont appelées « variables canoniques ». Mais les combinaisons linéaires sont des expressions mathématiques parfois dépourvues de sens physique si, dans un groupe, certaines variables sont « hors sujet » ou erronées. Des « corrélations canoniques » entre ces combinaisons ne fournissent donc pas toujours une clé d’interprétation.
« L’Iconographie des Corrélations » est au contraire facile à interpréter, car elle s’appuie uniquement sur les variables initiales. Les variables « hors sujet » ou erronées ont en général peu d’effet sur l’interprétation des autres variables.
Nous reprenons un exemple qui fut traité (ici) par les corrélations canoniques.
Conditions des règles de conduite routière
Gaymard [2007] a construit un questionnaire permettant d’identifier les conditions spécifiques dans lesquelles les conducteurs trouvent qu’il est acceptable de transgresser les règles.
Par exemple dans le cas du scénario du feu rouge : « il vous arrive de ne pas vous arrêter au feu rouge si le véhicule suivant vous colle...»
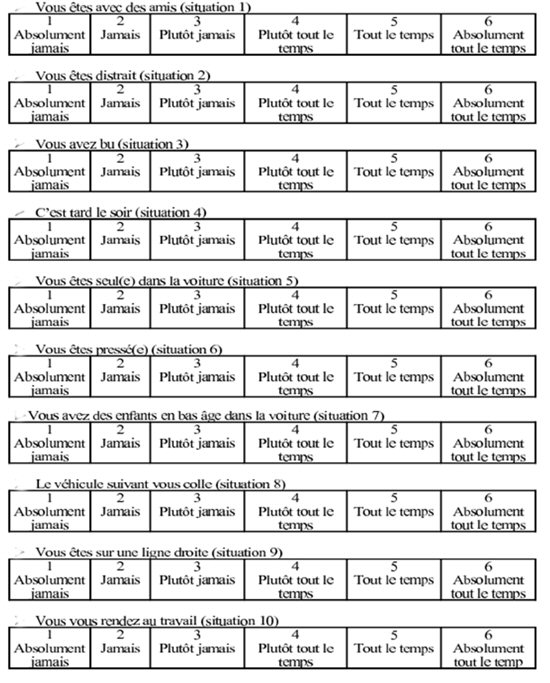
Le questionnaire recueilli auprès de 43 jeunes conducteurs (moyenne d’âge = 20, 24 ans)
D’après Gaymard Sandrine, « La représentation de la conduite chez les jeunes conducteurs.
Une étude de la conditionnalité routière », Recherche Transports Sécurité 97, 2007, p. 339-359.
L’article présente les résultats du questionnaire en trois tableaux séparés :
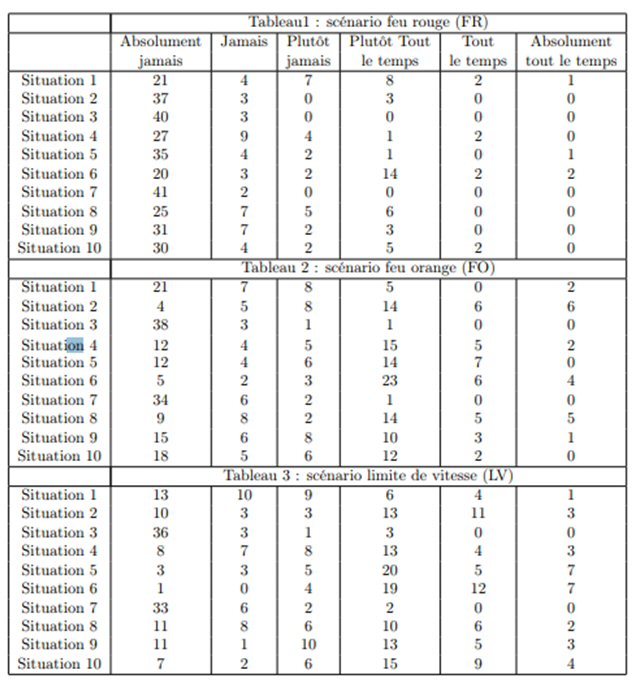
D’après « Les analyses canoniques simple et généralisée linéaires :
applications à des données psycho sociales."
Victor Nzobounsana et Sandrine Gaymard, 2010
L’analyse canonique considère chacun de ces trois groupes de données comme un tout représenté par des combinaisons linéaires des variables du groupe ; et les « corrélations canoniques » sont les corrélations entre ces combinaisons. L’hypothèse est que cette corrélation a un sens physique.
Or, dans la réalité, il se peut que certaine variable du groupe 1, soit liée à telle autre du groupe 2 ou du groupe 3, tandis qu’une autre variable du groupe 1 ne soit liée à aucune variable des autres groupes. C’est cela que nous avons besoin de savoir. Et pour le savoir, il faut rassembler les trois tableaux en un seul.
C’est pourquoi, l'iconographie des corrélations au contraire, pour ne faire aucune hypothèse, ne distingue pas les groupes, et rassemble les trois tableaux en un seul, soit en les empilant, soit on les juxtaposant.
Tableaux empilés en un seul
Tableau 2
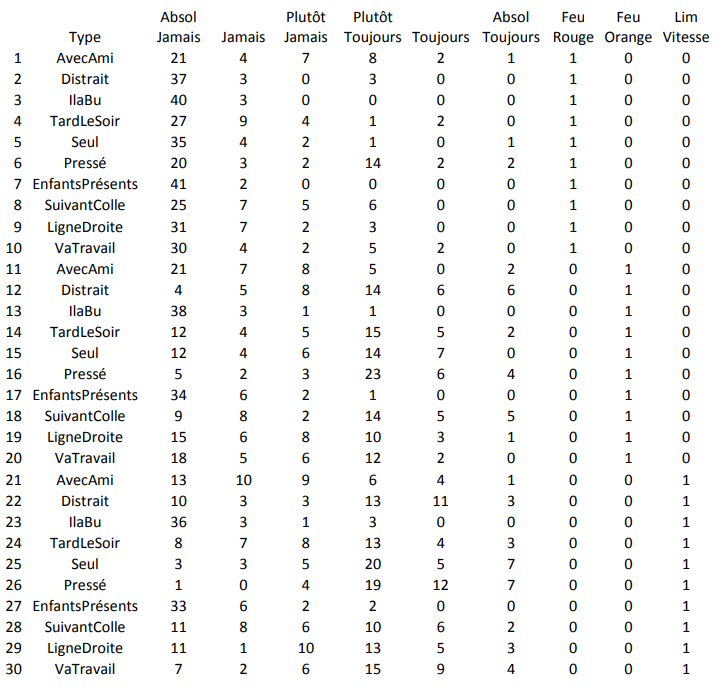
Les trois variables qualitatives de droite nous informent sur les trois scenarii possibles : Feu rouge, Feu orange ou Limite de vitesse. Voici l’Iconographie des Corrélations des colonnes de ce taleau :
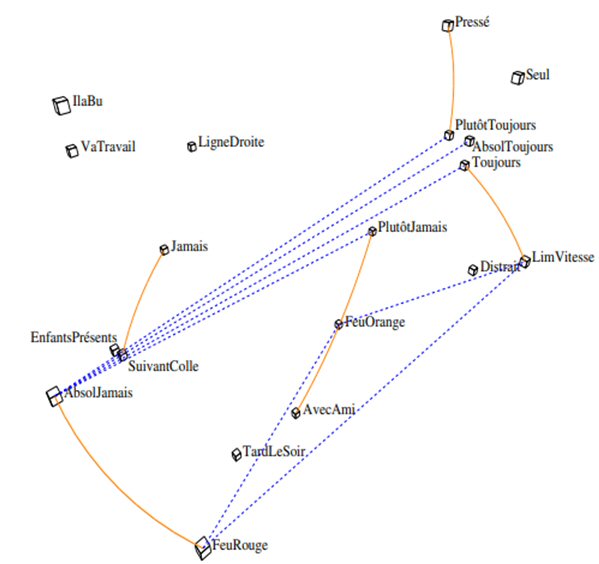
Figure 1 : Iconographie des corrélations au Seuil 0.3
Trait plein : lien positif « remarquable »; trait pointillé : lien négatif « remarquable »
Principe du schéma : le lien entre deux variables est dit « remarquable » (il est tracé) si la corrélation demeure supérieure au seuil quand n’importe laquelle des autres variables est constante.
Cette figure conserve les liens les plus « solides » : l’élimination des « fausses bonnes corrélations » est d’autant plus sévère que le nombre de variables est grand. Les résultats sont visuels et sans ambigüité :
Les autres cas de ne pas respecter les règles ne sont pas liés entre eux, au seuil 0.3.
Si on baisse le seuil à 0.1, d’autres liens apparaissent :
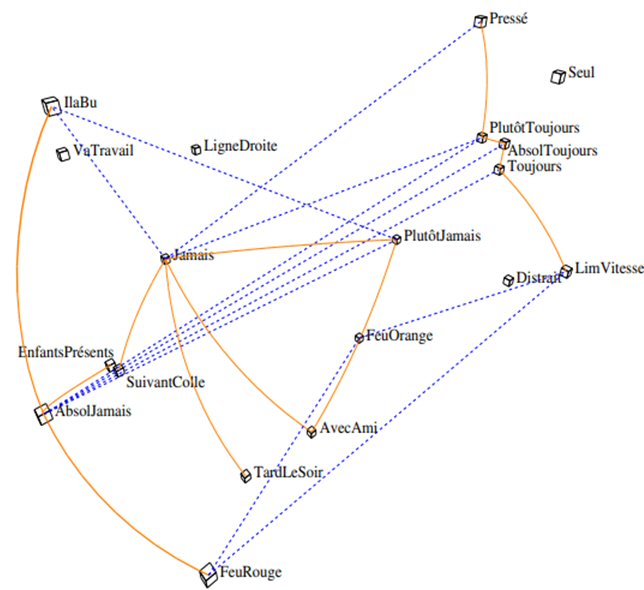
Figure 2 : Iconographie des corrélations au Seuil 0.1
Traits plein : Lien positif remarquable; traits pointillés : lien négatif remarquable
A ce seuil 0.1, les nouveaux liens sont :
Tableaux juxtaposés en un seul
Juxtaposons maintenant les trois scénarii : Feu rouge (FR), Feu orange (FO) et Limite de vitesse (LV) :
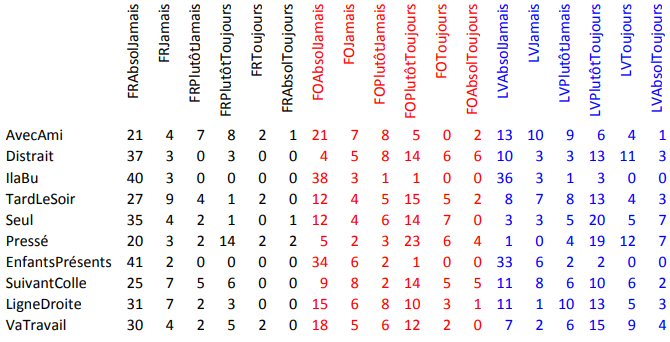
Voici l’Iconographie des Corrélations des colonnes de ce tableau :
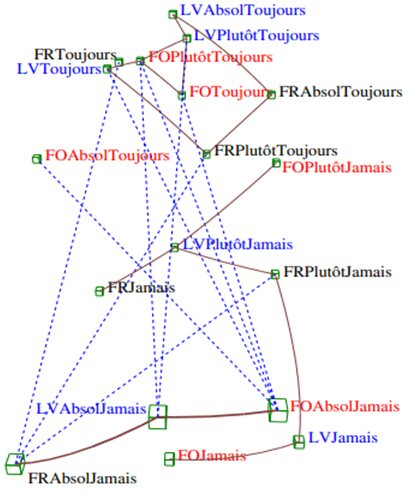
Figure 3 : Iconographie des corrélations entre les colonnes du tableau des trois scenarii juxtaposés, au seuil 0.3
Traits plein : Liens positif remarquables; traits pointillés : liens négatifs remarquables
On constate que toutes les sortes de « toujours » (en haut du dessin) s’opposent à toutes les sortes de « jamais » en bas du dessin : il y a opposition entre les transgressions et le respect de la règle. Les FR, FO et LV se ressemblent : les trois scenarii sont liés.
Rajout d’informations sur la figure
En Iconographie des corrélations, on peut rajouter, en éléments supplémentaires, les noms de lignes remarquables sur la figure précédente (c’est la notion « d’instants remarquables » expliquée dans ce livre broché, ou ce ebook) :
Seuls sont rajoutés les noms qui sont liés à une variable au moins.
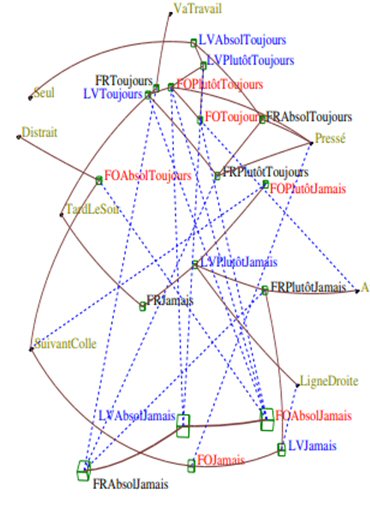
Figure 4
La figure 4 a rajoutées plusieurs informations concernant les lignes du tableau juxtaposé :
Corrélations entre les lignes du tableau juxtaposé
Si maintenant on analyse les corrélations entre les lignes du tableau juxtaposé :
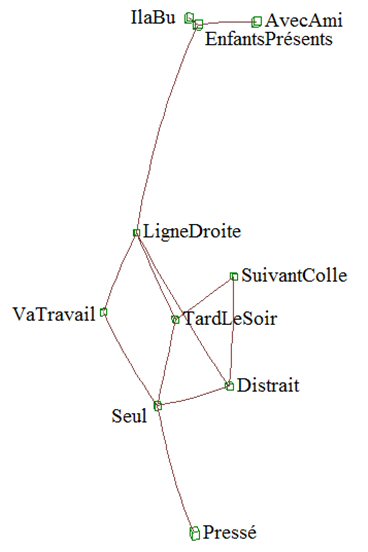
Traits plein : Liens positif remarquables; traits pointillés : liens négatifs remarquables
Cette figure distingue, en haut un groupe « Il a bu », « Enfants présents » et « Avec ami » plus propice au respect des règles ; et un groupe en bas du dessin, plus propice à la transgression.Toutefois le « Distrait » affirme ne brûler le feu rouge « absolument jamais ».
Intermédiaire entre ces groupes il y a « Ligne droite ».
Conclusion de l’analyse
L’Iconographie des Corrélations permet d’analyser les relations entre plusieurs ensembles de variables mesurées sur les mêmes individus. Plus visuelle et rapide que l’analyse canonique, elle évite la consultation de tableaux fastidieux de chiffres, et le recours à des « axes factoriels » (combinaisons linéaires des variables), souvent difficile à interpréter, car les variables « hors sujet » ou erronées répercutent leurs effets perturbateurs sur les axes et donc sur toute l’analyse.
Voir aussi :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.