Une alternative à l'analyse discriminante.
L'exemple des billets de banque contrefaits.
L’iconographie des Corrélations constitue une alternative simple et rapide à l’analyse discriminante. Voyons-le sur des données qui avaient été traitées par Analyse Discriminante ici.
Six mesures sont prises sur deux populations de billets de banque suisse : 100 billets authentiques et 100 billets contrefaits :

Voici le début du tableau d’apprentissage qui contient 200 lignes (100 vrais billets et 100 faux billets).
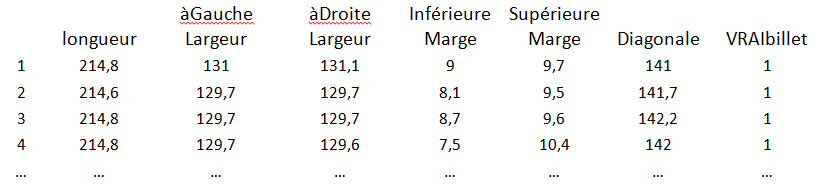
A partir de ces données, comment déterminer automatiquement si un nouveau billet est vrai ou contrefait? On essaiera deux méthodes : la régression multiple et l’iconographie des corrélations.
La variable « VRAIbillet » vaut 1 s’il est vrai et 0 s’il est faux.
L’iconographie des corrélations des colonnes du tableau
L’iconographie des corrélations des colonnes du tableau, nous donne une vue rapide des liens remarquables :
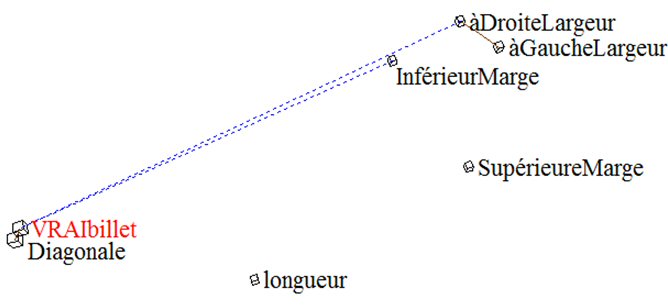
Figure 1 : Iconographie des corrélations des colonnes, Seuil 0.3
Trait plein : lien positif « remarquable »; trait pointillé : lien négatif « remarquable »
Principe du schéma : le lien entre deux variables est dit « remarquable » (il est tracé) si la corrélation demeure supérieure au seuil quand n’importe laquelle des autres variables est constante.
Les vrais billets ont une plus grande diagonale, une plus faible marge inférieure et une plus faible largeur à droite.
Si au lieu de « VRAIbillet » (qui vaut 1 si c’est vrai et 0 si c’est faux), nous avions défini la variable « FAUXbillet », qui vaut 1 si c’est faux et 0 si c’est vrai, nous aurions obtenu le schéma équivalent :
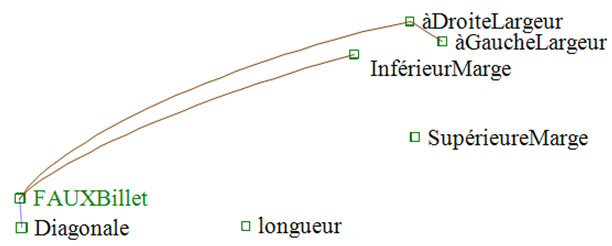
Figure 2 équivalente à la figure 1
Le nouveau billet est-il contrefait ?
Il s’agit maintenant de savoir si le billet suivant, de provenance inconnue, est contrefait ou non :
Modèles de régression
Une méthode de prédiction pourrait être la construction d’un modèle des vrais billets. Avec le logiciel CORICO, on trouve :
Modèle 1, sans interaction logique :
VRAIbillet = -40.14 + 0.2973 Diagonale - 0.1201 InférieurMarge
Modèle 2, avec interaction logique :
VRAIbillet = 0.5000 + 6.925 Diagonale}Diagonale
Le modèle 2 a un meilleur R2 ajusté.
Une partie seulement des mesures semble jouer un rôle : la diagonale et la marge inférieure. C’est ce qu’avait d’ailleurs montré l’iconographie des corrélations.
Dans les tableaux suivants, dans chaque ligne,
Dans la colonne « Choix », saisissons (en rouge) les valeurs du billet inconnu :
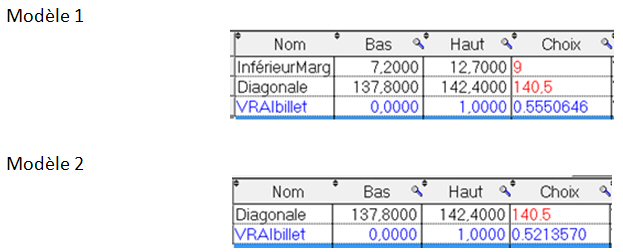
Pour ces valeurs, le modèle 1 de « VRAIbillet » prédit 0,5550645, et le modèle 2 prédit 0,5213570.
Dans les deux cas, on est au dessus du milieu entre vrai et faux ( 0.5) , donc ce serait plutôt un vrai billet. Cependant les valeurs prédites étant très proches de 0,5, le résultat est, à nos yeux, douteux.
Comme l’écrivent les auteurs de l’étude, « il faut penser aux conséquences d’une erreur. Classer un billet authentique comme une contrefaçon pourrait mettre une personne innocente en prison. L’erreur inverse risque de laisser un criminel en liberté. »
Le résultat de la méthode de régression étant indécis, essayons l’autre méthode : l’Iconographie des Corrélations entre les lignes.
L’Iconographie des Corrélations entre les lignes
Rajoutons une ligne au tableau de données : le billet « Inconnu » à prédire . Supprimons la colonne VRAIbillet. Puis transposons le tableau après réduction (le tableau est centré réduit pour s’affranchir des unités de mesures). Voici le résultat obtenu :
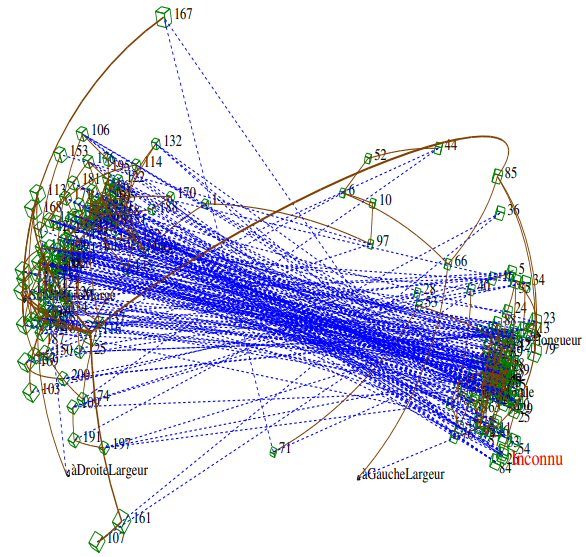
Figure 3 : Iconographie des corrélations des lignes, Seuil 0.3
Le billet inconnu en bas à droite en rouge.
Trait plein : lien positif remarquable ; trait pointillé : lien négatif remarquable
Deux groupes s’opposent (traits pointillés). L’inconnu est dans le groupe de droite, à coté de 54 et 84, qui sont des VRAIS billets. Les faux billets (numéros 101 à 200) sont à gauche.
Si, pour clarifier, on ne dessine que les liens à l’Inconnu, on voit qu’il n’a que des liens négatifs avec de gros numéros. :
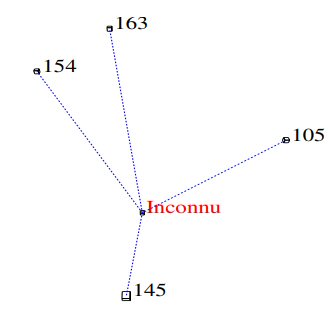
L’inconnu paraît donc très certainement un vrai billet.
CONCLUSION : La figure claire et distincte de l’iconographie des corrélations donne un résultat plus évident que le modèle de régression, et plus rapide et intuitif que l’analyse discriminante.
L’iconographie des corrélations permet la discrimination.
Voir aussi :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.