Corrélation « significative » ou corrélation « remarquable » ?
La « significativité » est relative à un modèle statistique, pas forcément observé dans la pratique.
Par suite « La signification statistique n’est pas équivalente à la signification scientifique, humaine ou économique » (R.L. Wasserstein et N.A. Lazar, « The ASA's Statement on p-Values: Context, Process, and Purpose », The American Statistician, vol. 70, no 2, 2 avril 2016, p. 129–133).
Or c’est la signification scientifique, humaine ou économique qui nous importe. Comment y arriver ?
Peut-on parler de « corrélation significative » ?
Considérons les poids de 8 élèves du collège, et leurs notes respectives en mathématique.
Le coefficient de corrélation est r(Poids, note) = 0.773
Cette valeur importante ne peut pas être expliquée par le hasard ou par des erreurs de mesures aléatoires :
Le poids et la note ne sont donc pas « aléatoires » pour les 8 élèves choisis. Le professeur s’intéresse à ses élèves particuliers, sans préjuger de résultats hypothétiques sur une population plus vaste d’élèves.
Suffit-il de mieux nourrir les élèves pour obtenir une bonne note ?
Accorder une signification à ce coefficient de corrélation pris isolément, c’est supposer toutes choses égales par ailleurs, ou que les influences extérieures s’annulent les unes les autres, et renoncer à explorer toutes les pistes pouvant expliquer les notes des 8 élèves.
On peut parfois s’intéresser à une différence statistiquement significative entre deux moyennes (par exemple, lors de la comparaison des effets d’un médicament et d’un placébo), mais cela a-t-il un sens de parler de corrélation significativement non nulle ?
La corrélation est un point de vue.
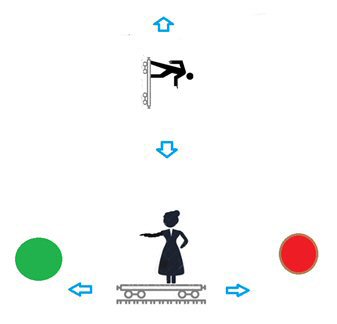
Madame X, dans le brouillard, aperçoit deux ballons lumineux :
La voix de Monsieur Y répond dans le brouillard :
Le brouillard se dégage. Madame X et Monsieur Y s’aperçoivent que chacun va et vient sur des planches à roulettes dont les trajectoires sont orthogonales.
Quand Madame s’approche du ballon vert, il semble grossir et le rouge diminuer : la corrélation vaut -1. Quand Monsieur s’approche du ballon vert, il s’approche aussi du rouge, et tous deux semblent grossir : la corrélation vaut +1.
En réalité, la taille des ballons reste constante. Dans l’absolu, il n’y a pas de corrélation. Les corrélations observées dépendent du point de vue. Si la planche à roulette se déplace sur une trajectoire oblique ou plus étendue, la corrélation peut avoir une valeur intermédiaire.
Faut-il conclure que le coefficient de corrélation est inutilisable ?
Oui, si le chiffre est isolé. Non, si l’on dispose des corrélations avec d’autres variables, car nous pourrons alors recouper les points de vue.
Recouper les points de vue.
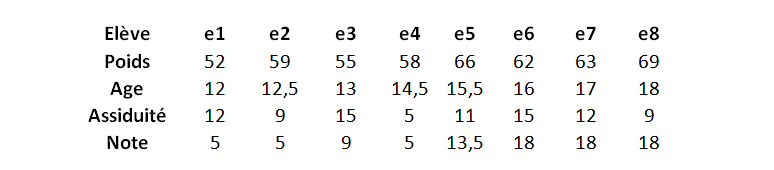
Nous aimerions savoir si la corrélation entre poids et note resterait forte, si tous les élèves avaient le même âge, ou si tous avaient la même assiduité. Malheureusement nous ne disposons que de 8 élèves, et ils ont tous un âge différent ! Comment faire ?
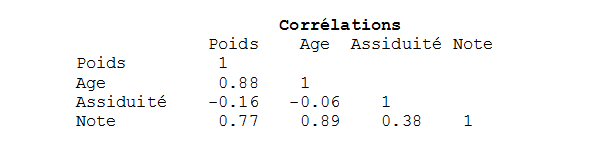
Il existe une formule mathématique qui, à partir des trois coefficients de corrélation r(Poids, Note), r(Poids, Age) et r(Age, Note), donne le coefficient de corrélation partielle entre Poids et Note si l’âge était resté constant (on se place du point de vue de l’âge) :
La corrélation a diminué drastiquement ! Elle est même légèrement négative : le lien entre le poids et la note n’est pas pertinent.
Par contre la corrélation du poids avec l’âge reste forte, même si l’on se place à Note constante :
De même la corrélation de la Note avec l’âge reste forte, même si l’on se place à Poids constant :
Concluons que les corrélations entre le poids et l’âge, ainsi qu’entre la note et l’âge sont des informations plus pertinentes (plus "remarquables") que la corrélation 0,77 observée entre le poids et la note. Cette dernière information est redondante et découle de l’influence de l’âge à la fois sur la note et sur le poids.
Qu’en est-il de la corrélation entre Poids et Note, si l’on se place à assiduité constante ?
La valeur de la corrélation partielle a augmenté par rapport à la corrélation totale, car l’assiduité a une influence seulement sur la note et pas sur le poids ; donc, si on se place à assiduité constante, on voit mieux la corrélation entre Poids et Note, ce qui n'implique pas forcément sa pertinence.
De même si l’on se place à Note constante, on renforce en valeur absolue, la corrélation négative entre Poids et Assiduité :
La formule mathématique du coefficient de corrélation est celle du cosinus. Toute corrélation, même nulle, apporte donc une information précise : une distance angulaire.
Voici les angles correspondants aux points de vue de l’âge et de l’assiduité :
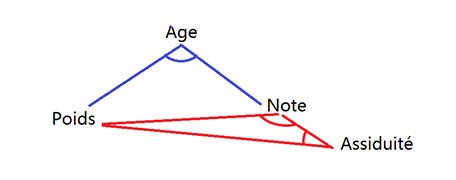
Les corrélations partielles autorisent de multiples points de vue, dont la confrontation permet de lever les doutes sur les proximités réelles, avec une précision trigonométrique.
Ainsi pouvons-nous juger du relief d’un paysage parce que la vision binoculaire présente chaque détail sous deux angles différents. Grâce au relief, nous connaissons que deux points qui semblaient proches sont en réalité éloignés l’un de l’autre.
Corrélations « remarquables »
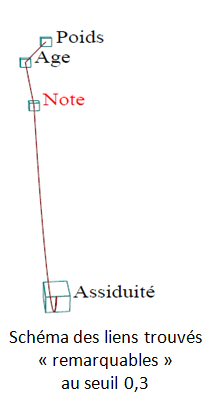
Considérée isolément, une corrélation même forte, n’apporte aucune information.
Il faut tenir compte du contexte. Alors, même une corrélation nulle est une information précise (angle droit).
Une corrélation est dite "remarquable", si
Le "contexte", ce sont donc les variables disponibles en plus des deux dont nous calculons la corrélation.
Un lien remarquable positif est représenté par un trait plein. Un lien remarquable négatif est représenté par un trait pointillé.
Tel est le principe de l’Iconographie des Corrélations.
Son efficacité découle de sa simplicité : la méthode n'est jamais une "boîte noire".
Le choix du seuil
Le choix du seuil s’apparente au réglage du volume sonore dans une chaîne Hifi. Il ne dépend pas de l’opinion d’un expert, mais du niveau de finesse requis à un moment donné par l’utilisateur. Le même utilisateur peut donc utiliser plusieurs seuils, et les résultats ne se contredisent pas.
A noter que même au seuil nul, le lien entre Poids et Note n’est pas tracé, puisque il existe une corrélation partielle de signe opposé à celui de la corrélation totale.
« Corrélation linéaire » : un abus de langage.
Ne pas confondre « corrélation », dont la mesure dépend du point de vue, et « relation » qui est un phénomène physique sous-jacent (un lien remarquable).
Soient des variables indépendantes A, B, C, D, E, F, G. et supposons : Y = A + B + C + D + E + F + G.
La corrélation de Y est faible avec chacune des 7 variables explicatives ; et pourtant la relation de Y est strictement linéaire avec chacune d’entre-elles. La corrélation ne vaut 1 avec l’une d’elles que quand les 6 autres sont constantes, c’est-à-dire toutes choses égales par ailleurs.
L’adjectif « linéaire » est inapproprié pour un cosinus (et donc pour un coefficient de corrélation), c’est la relation qui est multilinéaire ici.
Et si le seuil est suffisamment bas, l’Iconographie des Corrélations donnera un lien de Y avec chacune des 7 variables.
La table de signification du coefficient de corrélation de Pearson, qui donne des valeurs critiques en fonction du nombre d’observations, n’est pas appropriée : des relations non pertinentes (non physiques, comme le lien du poids et de la note) seraient conservées à tort, tandis que des liens remarquables pourraient être écartés.
Conclusion
La statistique probabiliste s’est d’abord développée, à partir de une ou deux variables aléatoires (jeux de hasard : pile ou face, roulette, dés...).
D’où l’importance accordée aux notions de significativité des moyennes et de distributions statistiques, faute d’informations sur le contexte.
Mais en réalité les variables influentes sont nombreuses.
Loin de compliquer l'interprétation, la prise en compte d'un grand nombre de variables facilite les recoupements, en évitant le recours aux hypothèses (et aux tests de ces hypothèses).
Avant d’aventurer une hypothèse, il convient en effet de procéder à un état des lieux aussi exhaustif que possible.
Approche géométrique non probabiliste, l'Iconographie des Corrélations offre une cartographie précise des données disponibles, par triangulation.
On compare toujours avec profit les résultats de plusieurs études conduites de cette façon, même (et peut-être surtout) si les résultats sont différents, car ils reposent sur du réel.
Il est en effet dommage que des données de haute qualité, collectées à des coûts importants, restent en grande partie non exploitées, pour cause de « non significativité » vis-à-vis de modèles prématurés.
Pour un exposé complet, assortis d'exemples, des avantages de l'approche géométrique des matrices de corrélations, procurez-vous le livre : "L'Analyse de Données par Iconographie des Corrélations", Michel Lesty, Ed. Monbeaulivre, 200 pages.
D'autres exemples d'iconographie des corrélations :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.
Economisez des années en Recherche et Développement :
INDUSTRIE - RECHERCHE - QUALITÉ - ÉPIDÉMIOLOGIE - ENQUÊTES - ECONOMETRIE ...
FORMATION
- Découvrir et maîtriser
- l'Analyse de Donnéees
- le Plan d'expériences
- les Séries Temporelles
- Voir les formations