L’interprétation des données brutes
une opération naturelle

La méthode de Madame Martin

Madame Martin assise à sa fenêtre contemplait l’arbre, les oiseaux, la maison du voisin. De temps en temps elle inscrivait des chiffres sur un cahier. Arrive Jean, son petit-fils.

- Grand-mère ! 7h30, 8h30, 19h, 21h… qu’est-ce que tu écris ?
- Tous les jours, Je note les sorties du voisin.
- Attends, je vais calculer la moyenne !

Jean sort sa calculette.

- 13h30, c’est son horaire moyen de sortie !
- Il ne sort jamais à 13h30, il doit faire la sieste.
- Ah ! La distribution n’est pas gaussienne !
- Quoi ?
- J’ai appris ça à l’école. Ca veut dire que la distribution n’est pas « normale ». Que veux-tu tirer de ces données ?
- Qu’est-ce que tu dis, Jean ! C’est tout à fait normal ! A 7h30 il va faire son jogging. A 8h30, il part au travail. A 21h, il va jardiner…
- Mais Grand-mère, comment le sais-tu ?
- A 7h30, il est en basket et en short. A 8h30, il porte un complet… A 21h il tient un râteau et un sécateur, c’est simple.
- Ah ! Tu fais une analyse multivariée !
- Multivarié ou pas, c’est quand même plus simple que ces histoires de moyenne ou de distribution !

Le cahier de Madame Martin

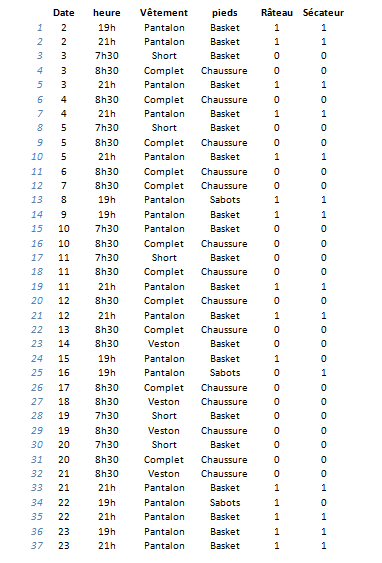
Une opération naturelle

Evidemment ! Sans le savoir, nous faisons tous de « l’analyse multivariée » : une contemplation coordonnée des choses. Dans la vie courante, il est plus facile de tenir compte de toutes les informations disponibles que d’interpréter une moyenne.

Si la distribution n’est pas « normale », que peut-on tirer d’une moyenne ?

Et si elle est « normale », la moyenne hors de son contexte nous renseigne peu. Son calcul est un pis-aller lorsqu’on ne dispose que d’une ou deux variables. Une décision basée sur des chiffres, même exacts, n’est pas forcément valide.

Autrement dit, La fiabilité et la facilité de l’interprétation des données brutes augmentent avec le nombre de variables relatives au contexte.

Dès l’enfance, nous sommes à chaque instant confronté à une foule d’informations disparates, et nous les exploitons sans connaissance mathématiques. A vrai dire, nous sommes tous « experts » en analyse multivariée.

De la mise en ordre des relations entre ces informations, sans supposer un modèle à priori, découle le plus souvent une interprétation correcte.

L'iconographie des corrélations du logiciel CORICO est basée sur cette idée : préparer le terrain de l’interprétation et de la prise de décision. Car « au sein du désordre la pensée ne sert de rien » (Paul Valéry).

L'iconographie des corrélations

L’iconographie des corrélations remplace la matrice de corrélation par un graphe unique, concis et intuitif.

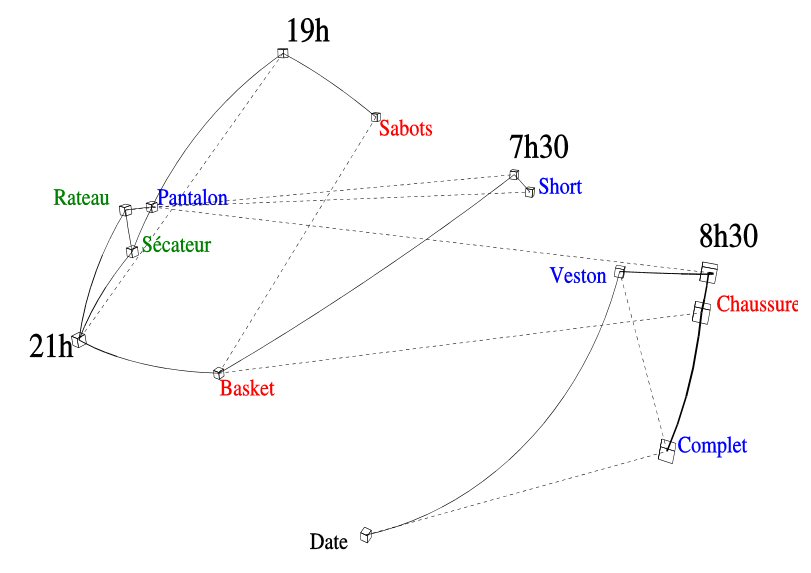
Iconographie des corrélations des données de Madame Martin au Seuil 0.1
Trait plein : corrélation positive « remarquable »
Trait pointillé : corrélation négative « remarquable »

Un principe d’interprétation simple : Une corrélation est dite « remarquable » si elle reste supérieure au seuil quand n’importe quelle des autres variables est constante.

Les liens douteux sont effacés. Une corrélation « significative » n’est donc pas forcément « remarquable ».

Aucune ambiguïté dans l’interprétation des liens de la figure :

Comparaison avec l’analyse en composante principale (ACP)

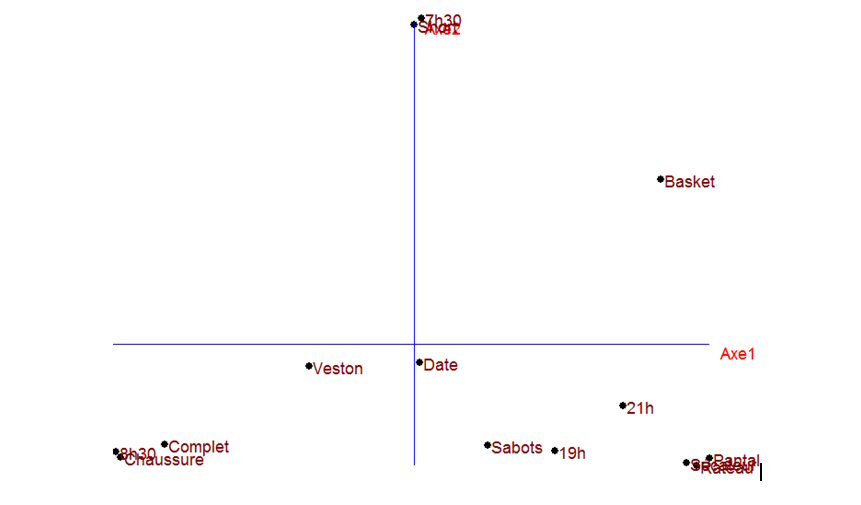
Analyse en Composantes Principales, axes 1 et 2

L'Analyse en Composantes Principales est un autre type d'analyse multivariée. C'est la projection du nuage de points dans le plan où le nuage s'étale le plus.

Ici, en l'absence de liens, l’interprétation est moins nette. Elle le serait encore moins si les variables étaient plus nombreuses. Car il est souvent difficile, même pour un expert, d’interpréter les axes factoriels.

Les points forts de l’iconographie des corrélations

L'analyse multivariée est paradoxalement plus simple que l’analyse univariée, et plus efficace car plus proche de la réalité du contexte considéré.

Le nombre d'observations n'est pas nécessairement grand (on peut travailler dès 4 observations).

Augmenter le nombre de variables relatives au contexte, loin de compliquer l'analyse, la simplifie au contraire !

Si le nombre de variables est grand, nous pouvons ne tracer que les liens à la variable d’intérêt : la figure devient claire, mais l’étude est sûre car elle a tenu compte de toutes les variables.

Le but est de tirer d’abord le meilleur parti des données disponibles, sans généraliser à un plus grand échantillon, c’est-à-dire sans demander à l’enquête de terrain plus qu’elle ne peut donner.

CORICO, d'un clic, débroussaille vos données. A vous d'en interpréter l'image.

Voir aussi :

---

Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.