La classification croisée : ranger lignes et colonnes
La classification croisée (appelée aussi bi-partitionnement, co-clustering ou biclustering) consiste à ranger d’une autre manière les lignes et les colonnes d’un tableau de données.
Classification croisée non supervisée

Comment a-t-on obtenu ici le rangement des colonnes ?
Même principe pour ranger les lignes, à partir de la matrice de corrélation des lignes.
Lorsque les colonnes ont des unités différentes, par exemple température, pression, latitude, etc., il est préférable de ramener les variables à une unité commune (par exemple centrer réduire les variables), sinon le classement des lignes dépendra des unités choisies.
Ce classement croisé est « non supervisé » car il ne privilégie aucune colonne ni aucune ligne.
Inconvénients :
Classification croisée K-means
Une méthode classique est la classification K-Means sur les lignes et sur les colonnes :
On recommence les étapes 1, 2 et 3 tant que les individus sont réaffectés à de nouveaux groupes après une itération.
Avantage : Les temps de calcul sont faibles. K-means peut donc être utilisée sur des volumes de données importants.
Inconvénients :
CORICO offre cependant la possibilité de ne pas tirer au hasard les centres initiaux. Le nombre K est trouvé automatiquement.
Classification croisée fine non supervisée
Une classification non supervisée plus générale, sans recours à des sommes, repose sur l’idée que plus deux colonnes sont corrélées, plus elles doivent être proches (même chose pour les lignes). Dans l’exemple ci-dessous, une classification croisée fine révèle six groupes :
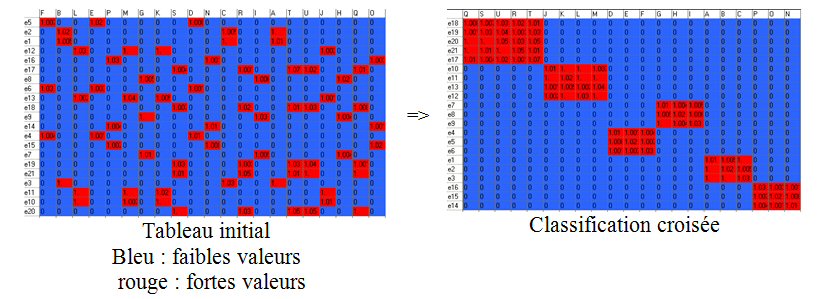
La Méthode s'apparente à la reconstitution soignée d'un puzzle où chaque élément, même le plus petit, a son importance.
Le coefficient de corrélation est la seule formule mathématique nécessaire. La Classification Croisée Fine détermine à chaque étape si une colonne (ou un groupe de colonnes), doit être placée à droite ou à gauche des colonnes précédemment rangées. Même chose pour les lignes.
Il ne s'agit donc pas, comme dans d'autres méthodes de Classification Croisées, de minimiser une somme de sommes. Dans Corico on cherche seulement à minimiser le temps de calcul et à autoriser le traitement de gros fichiers.
Un autre exemple sur un plus gros tableau montre la précision de la classification croisée fine par rapport à la classification croisée basée sur des sommes de corrélations :
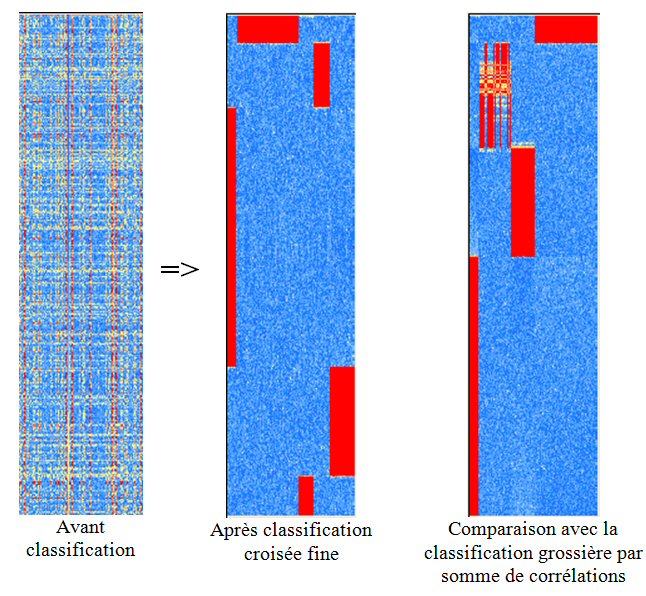
Inconvénient : cette méthode est moins rapide que K-means;
Avantages de la classification croisée fine :
Deux autres exemples de classification croisée fine non supervisée, avec à gauche des groupes emboîtés, et à droite des chevauchements de groupes:
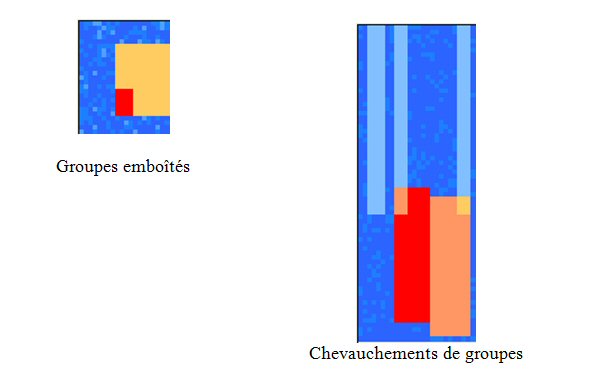
Classification croisée supervisée
Pour éviter les sommes, nous pouvons aussi superviser la classification en fonction d’une colonne et d’une ligne particulière.
Par exemple selon la colonne 3 croissante et la ligne E croissante :
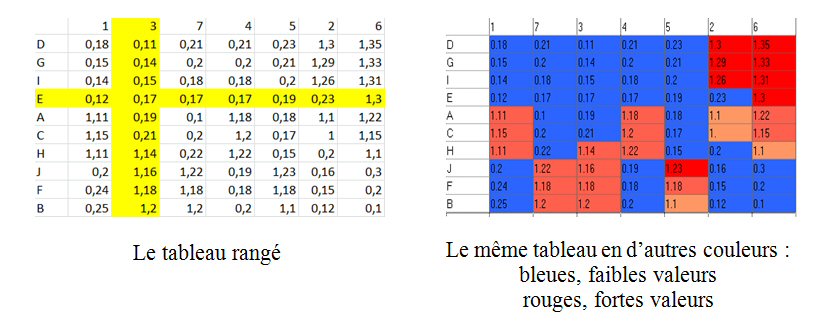
Ou bien, classification des colonnes selon leurs corrélations croissantes à la colonne 3, et classification des lignes selon leurs corrélations croissantes à la ligne E :
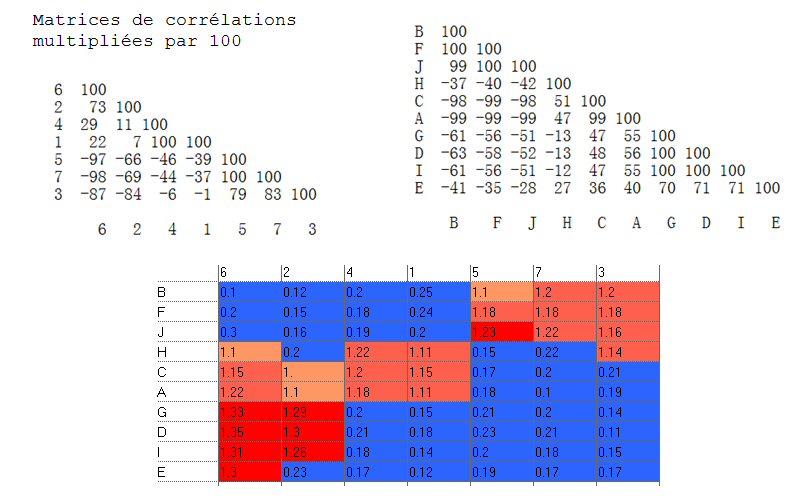
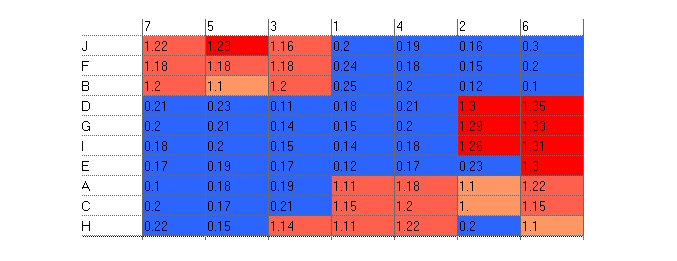
Ou bien encore, classification des colonnes selon les corrélations croissantes à la colonne 6, et classification des lignes selon les corrélations croissantes à la ligne H :
Limites de la classification croisée
Le classification croisée peut avoir une utilité pratique sur les tableaux simples. Mais, si peu de colonnes ou lignes se ressemblent, ou si des variables sont liées à plus de 2 variables indépendantes, la classification croisée donnera un piètre résultat.
Pour une classification plus rigoureuse et plus féconde, mieux vaut se tourner alors vers des méthodes graphiques plus générales. Exemple.
La classification croisée, qui est une représentation en deux dimensions, se prête mal à certains tableaux. Considérons par exemple les 24 permutations de 1,2,3,4 :

Aucune des 3 classifications ci-dessus n’améliore la présentation des données.
Au contraire une iconographie des corrélations, méthode multidimensionnelle, fait nettement apparaître l’organisation régulière de ces données :
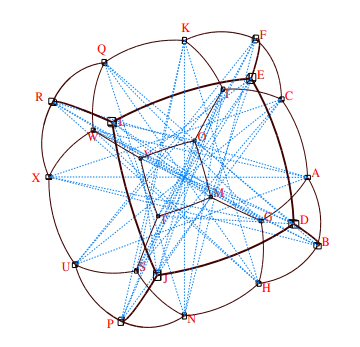
Aucune ambiguïté dans l'iconographie des corrélations : chaque lien « remarquable » est souligné ici par un trait plein (corrélation positive) ou pointillé (corrélation négative).
La variable X par exemple est liée positivement à 3 variables (traits pleins), lesquelles ne sont pas liées entre elles. X est aussi liée négativement à 4 variables (traits pointillés).
Au contraire, le rangement des colonnes (ou des lignes) par classification croisée ne permet pas une vue multidimensionnelle : car une colonne n’est jamais voisine à plus de deux colonnes. Et l’aspect négatif n’est pas considéré explicitement.
En iconographie des corrélations, quelle que soit la dimension des données, il est possible de représenter des liens à un nombre quelconque de variables, donc d’approcher la réalité où une variable ou une décision dépendent fréquemment de plusieurs facteurs indépendants.
En résumé, l’intérêt de la classification croisée est de classer à la fois les lignes et les colonnes et de mettre en évidence des groupes homogènes, mais on ne peut lui demander plus qu’elle ne peut donner.
Un exemple sur données réelles : les Poissons d’Amiard
Les données « Poissons d’Amiard » sont tirées de CAILLIEZ F., PAGES J.P. (1976), Introduction à l’analyse des données, SMASH.
Vingt-quatre mulets (sorte de rougets) sont répartis dans trois aquariums radio-contaminés de façon identique, à quoi correspondent des durées de contact différentes avec le polluant radioactif :

Dans ce qui suit, les 3 aquariums radio-contaminés seront notés « Un », « Deux » et « Trois ». « 13Deux » signifie poisson n°13 dans l’aquarium Deux, etc. « YeuxRA » signifie radioactivité des Yeux, etc.
Après avoir ramené les colonnes du tableau à une unité commune, commençons par une classification croisée fine non supervisée ; nous obtenons le Tableau 2.
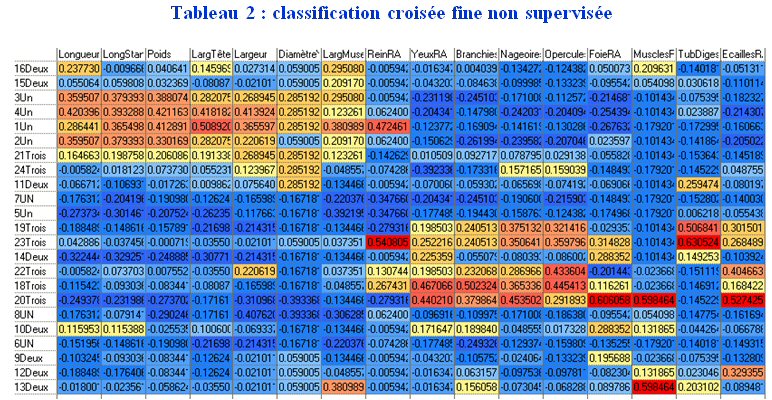
Procédons aussi à une iconographie des corrélations, qui ne repose, elle non plus, sur aucune hypothèse sur les données disponibles, ni aucun calcul de moyenne.
Le but d’une iconographie des corrélations est d’élaguer l’accessoire pour se concentrer sur l’essentiel : aspects généraux et points atypiques. L’interprétation repose sur les liens tracés plus que sur les positions.
Son principe est simple : le lien entre deux variables est dit « remarquable » (il est tracé) si la corrélation subsiste quand n’importe laquelle des autres variables disponibles est constante. En outre, un lien qui ne serait dû qu’à une observation n’est pas tracé.
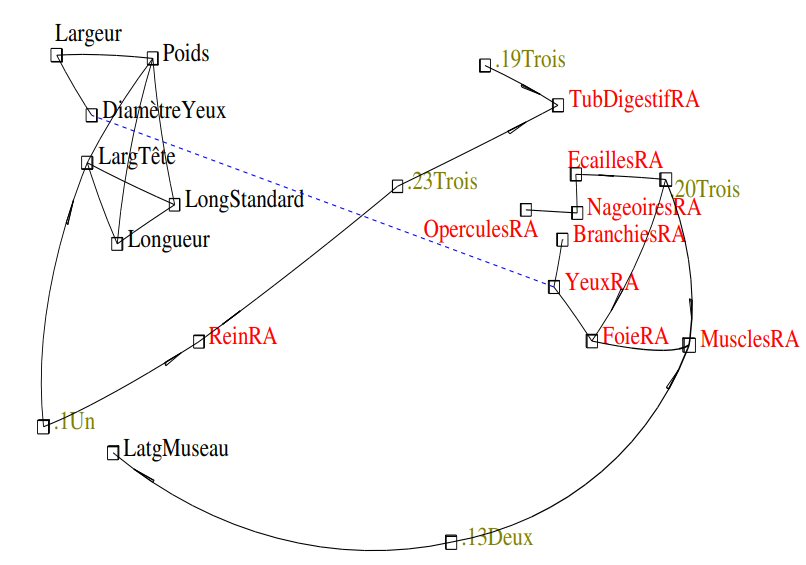
Figure 1 : Iconographie des corrélations, au seuil 0.3. Trait plein : corrélation « remarquable » positive ; pointillé : corrélation « remarquable » négative.
Deux groupes apparaissent :
Ces deux groupes s’opposent : la corrélation négative (ligne pointillée) entre le diamètre des yeux et la radioactivité des yeux signifie que lorsque les yeux sont grands leurs radioactivité est plus faible. Et comme le diamètre des yeux est lié à la largeur du poisson, elle-même liée à son poids, nous pouvons conclure que plus la taille du poisson est grande, moins ils sont radio contaminés ; ou encore que les petits poissons sont plus contaminés, peut-être parce que leur jeunesse les rend plus fragiles ; ou que la radioactivité influe sur la taille des poissons.
D’autre part, cinq poissons atypiques apparaissent sur la figure 1 :
Classification croisée supervisée
La différence observée entre petits et gros poissons nous conduit à superviser la classification croisée des colonnes par les corrélations au poids des poissons d’une part, et la classification des lignes par les corrélations au poisson « 4UN » qui est le plus lourd, d’autre part (tableau 3).
(Il se trouve qu’ici on obtiendrait une classification croisée identique au tableau 3 en classant non d’après les corrélations mais d’après les valeurs du tableau, en unité commune.)
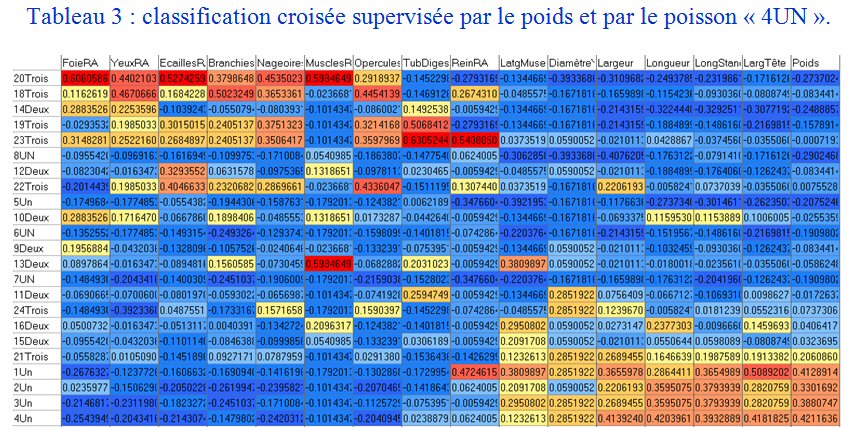
Le tableau 3 confirme les fortes radioactivités des petits poissons : le groupe jaune-orange en bas à droite correspond aux fortes tailles de poissons. Le groupe rouge-orange en haut à gauche correspond aux fortes radioactivités.
On retrouve les points atypiques remarquables de la figure 1 :
Influence des Aquariums
Jusqu’ici l’influence des aquariums n’est pas flagrante. Pour y voir plus clair ajoutons au tableau trois variables indicatrices des aquariums : la variable « UN » vaudra 1 si c’est l’aquarium 1, et 0 sinon ; la variable « DEUX » vaudra 1 si c’est l’aquarium 2, et 0 sinon ; la variable « TROIS » vaudra 1 si c’est l’aquarium 3, et 0 sinon.
Procédons ensuite à une iconographie des corrélations (figure 2).
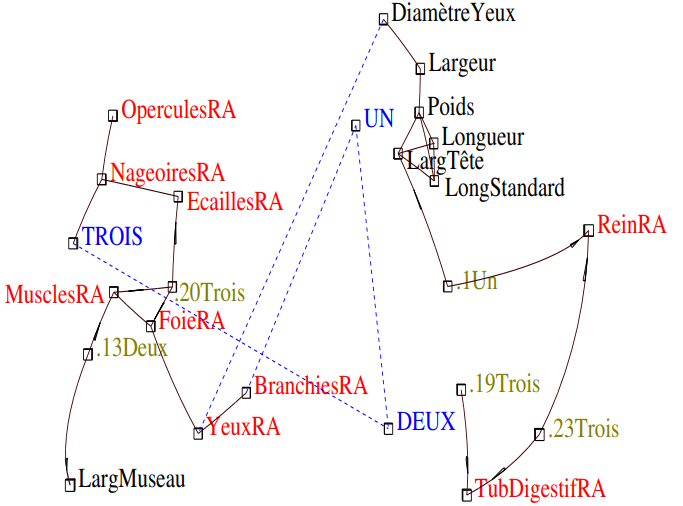
Figure 2 : Iconographie des corrélations au seuil 0.3, Après ajout des aquariums « UN », « DEUX » et « TROIS ».
Trait plein : corrélation remarquable positive ; trait pointillé : corrélation remarquable négative.
On retrouve dans la figure 2 les informations de la figure 1, avec en plus les informations suivantes :
Voir aussi :
D'autres exemples d'analyse de données avec le logiciel CORICO :
Vous êtes enseignant : contactez-nous pour connaître les conditions spéciales qui vous permettront d'équiper votre classe, votre laboratoire, votre école ou votre université.